Trigonometric functions: characteristics of sine, cosine and tangent

The sine function, $sin(x)$

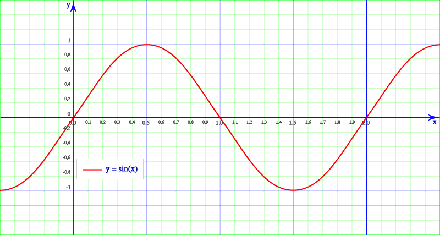
1. Domain: $\mathbb{R}$
2. Image: $[-1,1]$
3. Period: $2\pi$ rad
4. Continuity: It is continuous on $\mathbb{R}$
5. Increasing on: $\dots \cup ({\displaystyle -\frac{\pi }{2},\frac{\pi }{2})\cup ({\displaystyle \frac{3\pi }{2},\frac{5\pi }{2})\cup \dots }}$
6. Decreasing on: $\dots \cup ({\displaystyle \frac{\pi }{2},\frac{3\pi }{2})\cup ({\displaystyle \frac{5\pi }{2},\frac{7\pi }{2})\cup \dots }}$
7. Maxima at: $\{{\displaystyle \frac{\pi }{2}+2\pi \cdot k}$, $k\in \mathbb{Z}\}$
8. Minima at: $\{{\displaystyle \frac{3\pi }{2}+2\pi \cdot k}$, $k\in \mathbb{Z}\}$
9. Parity: Odd, $\sin x=-\sin (-x)$
10. Points of intersection with the axis Ox: $x=k\cdot \pi$, $k\in \mathbb{Z}$

The cosine function, $cos(x)$

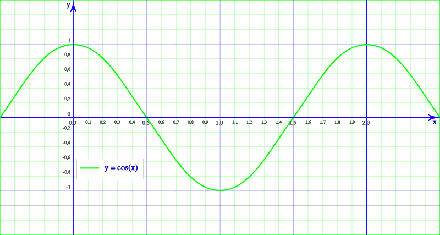
1. Domain: $\mathbb{R}$
2. Image: $[-1,1]$
3. Period: $2\pi$ rad
4. Continuity: It is continuous on $\mathbb{R}$
5. Increasing on: $\dots \cup (-\pi ,0)\cup (\pi ,2\pi )\cup \dots$
6. Decreasing on: $\dots \cup (0,\pi )\cup (2\pi ,3\pi )\cup \dots$
7. Maxima at: $\{2\pi \cdot k$, $k\in \mathbb{Z}\}$
8. Minima at: $\{\pi \cdot (2k+1)$, $k\in \mathbb{Z}\}$
9. Parity: Pair $\cos x=\cos (-x)$
10. Points of intersection with the axis Ox: $x={\displaystyle \frac{\pi }{2}+k\cdot \pi }$, $k\in \mathbb{Z}$

The tangent function, $tan(x)$

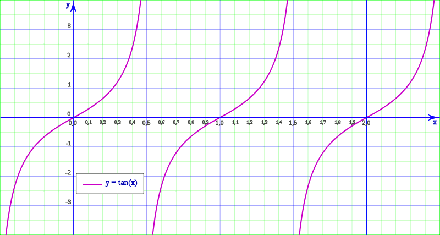
1. Domain: $\mathbb{R}-\{(2k+1)\cdot {\displaystyle \frac{\pi }{2},k\in \mathbb{Z}\}=\mathbb{R}-\{\dots ,{\displaystyle -\frac{\pi }{2},\frac{\pi }{2},\frac{3\pi }{2},\dots \}}}$
2. Image: $\mathbb{R}$
3. Period: $\pi$ rad
4. Continuity: It is continuous on $\mathbb{R}-\{{\displaystyle \frac{\pi }{2}+k\pi ,k\in \mathbb{Z}\}}$
5. Increasing on: $\mathbb{R}$
6. Maxima: No maxima
7. Minima: No minima
8. Parity: Odd $\tan x=-\tan (-x)$
9. Points of intersection with the axis Ox: $x=k\cdot \pi ,k\in \mathbb{Z}$