Tales'theorem

This is the basic theorem of similarities.

The Tales' theorem says: If two straight lines, not necessarily parallel, are cut by a system of parallel lines, then the resultant segments on one of the two lines are proportional to the respective segments obtained on the other line.

A figure to illustrate the above statement:

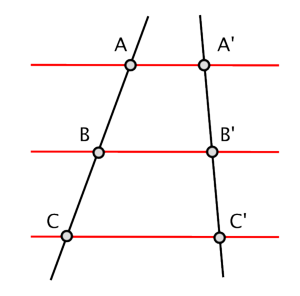
imagen

it is satisfied that $\frac{A B}{A^{'} B^{'}} = \frac{B C}{B^{'} C^{'}} .$

Example

For example, given the following figure, decide whether the resultant segments are similar or not.

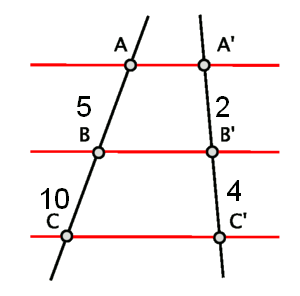
imagen

As we can see in the figure, the segment lengths are as follows: $(A B = 5, A^{'} B^{'} = 2)$ ; $(B C = 10, B^{'} C^{'} = 4)$ . By Tales'theorem, we can say that the segments among straight lines are similar because the ratios are equal:

$\frac{A B}{A^{'} B^{'}} = \frac{5}{2} = \frac{10}{4} = \frac{B C}{B^{'} C^{'}}$

Finally, we give an application that can be useful for solving certain exercises. Thanks to Tales' Theorem, we can calculate the height of an object, for example, a tree, by the following mechanism.

Let $C$ be the length of the shadow of the tree at a certain time.
Let $B$ be the length of the shadow of a small object, for example a pencil, at the same instant.
Let $A$ be the height of the pencil.

Then, it is satisfied that the height of the tree, called $H$ , is given by the following equation: $H = C \cdot (\frac{A}{B})$