Éste es el teorema básico de las semejanzas.
El Teorema de Tales dice: Si dos rectas, no necesariamente paralelas, son cortadas por un sistema de rectas paralelas, entonces los segmentos que resultan sobre una de las dos rectas son proporcionales a los correspondientes segmentos obtenidos sobre la otra.
A continuación, damos una figura para ejemplificar el enunciado anterior:
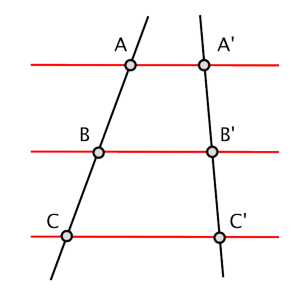
dónde se cumple que $$\dfrac{AB}{A'B'}=\dfrac{BC}{B'C'}.$$
Por ejemplo, dada la figura siguiente, decidir si son o no semejantes los segmentos resultantes.
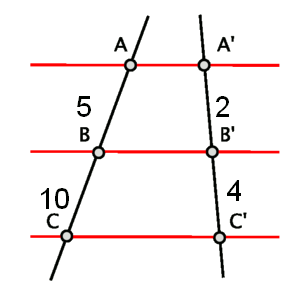
Como observamos en la figura, las longitudes de los segmentos son los siguientes: $$(AB = 5, A'B' = 2)$$; $$(BC = 10, B'C' = 4)$$. Por el Teorema de Tales, se ve que los segmentos de una recta y otra son semejantes gracias a que las razones son iguales:
$$$\dfrac{AB}{A'B'}=\dfrac{5}{2}=\dfrac{10}{4}=\dfrac{BC}{B'C'}$$$
Para terminar, vamos a dar una aplicación que puede resultar muy útil para la resolución de determinados ejercicios. Gracias al Teorema de Tales, podemos calcular la altura de un objeto, por ejemplo, un árbol, mediante el siguiente mecanismo.
- Sea $$C$$ la longitud de la sombra del árbol a una determinada hora.
- Sea $$B$$ la longitud de la sombra de un objeto pequeño, por ejemplo un lápiz, en el mismo instante.
- Sea $$A$$ la altura del lápiz.
Entonces, se cumple que la altura del árbol, llamada $$H$$, se obtiene mediante la siguiente igualdad: $$$H=C\cdot\Big(\dfrac{A}{B}\Big)$$$
