Teorema de Tales

Aquest és el teorema bàsic de les semblances.

El Teorema de Tales diu: Si dues rectes, no necessàriament paral·leles, són tallades per un sistema de rectes paral·leles, llavors els segments que resulten sobre una de les dues rectes són proporcionals als corresponents segments obtinguts sobre l'altra.

A continuació, mostrem una figura per exemplificar l'enunciat anterior:

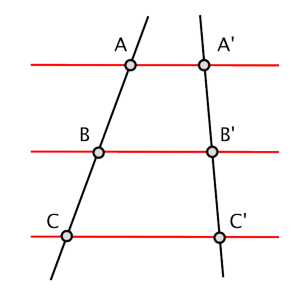
imagen

on es compleix que ABA′B′=BCB′C′.

Exemple

Per exemple, donada la figura següent, decidir si són o no semblants els segments resultants.

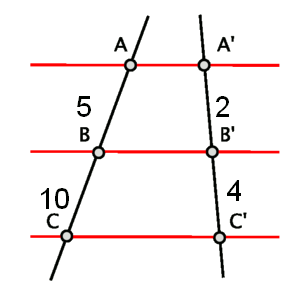
imagen

Com observem en la figura, les longituds dels segments són les següents: (AB=5,A′B′=2); (BC=10,B′C′=4). Pel Teorema de Tales, es veu que els segments d'una recta i una altra són semblants gràcies al fet que les raons són iguals,

ABA′B′=52=104=BCB′C′

Per acabar aquesta secció, donarem una aplicació que pot resultar molt útil per a la resolució de determinats exercicis. Gràcies al Teorema de Tales, podem calcular l'alçada d'un objecte, per exemple, un arbre, mitjançant el següent mecanisme.

  1. Sigui C la longitud de l'ombra de l'arbre a una determinada hora.
  2. Sigui B la longitud de l'ombra d'un objecte petit, per exemple un llapis, en el mateix instant.
  3. Sigui A l'altura del llapis.

Llavors, es compleix que l'alçada de l'arbre, que anomenem H, s'obté mitjançant la següent igualtat: H=C⋅(AB)