Se define la función de probabilidad de la variable aleatoria $$X$$ como la que asocia una probabilidad $$p_i$$ a cada valor posible de $$X$$ $$(x_1,x_2,\ldots,x_n)$$. Respecto a las probabilidades, se cumple siempre que: $$$\begin{matrix}0 \leq p_i\leq 1 \\ p_1+p_2+p_3+ \ldots +p_n= \sum_{i} p_i=1\end{matrix}$$$
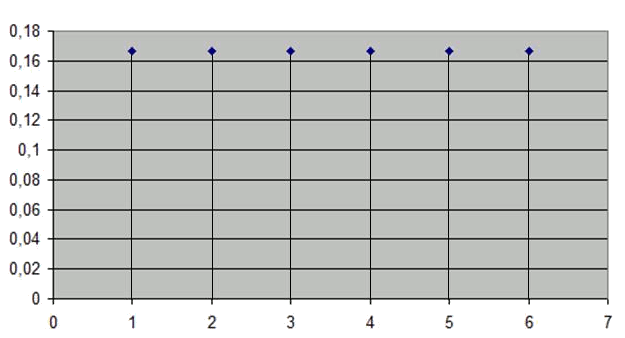
La variable aleatoria $$X$$ es el resultado de tirar un dado. Suponiendo que las seis caras del dado son equiprobables, las probabilidades de cada resultado son: $$$\displaystyle p(X=1)=P(X=2)=\ldots=P(X=6)=\frac{1}{6}$$$ Se puede comprobar que se cumple que $$$\displaystyle \sum_{i} p_i=6 \cdot \frac{1}{6}=1$$$ El gráfico de dicha función tiene forma de diagrama de barras: