La función distribución de una variable aleatoria $$X$$ es una función que proporciona, en cada punto, la probabilidad acumulada hasta dicho valor. Es decir:
$$$F(X)=p(X \leq x)$$$
Por ejemplo, se estudia la función distribución de la variable aleatoria $$X$$, resultado de tirar un dado perfecto.
La siguiente tabla muestra los valores de $$F (x)$$:
| x | F (x) |
| $$x < 1$$ | $$0$$ |
| $$1\leq x < 2$$ | $$\displaystyle \frac{1}{6}$$ |
| $$1\leq x < 3$$ | $$\displaystyle \frac{2}{6}$$ |
| $$1\leq x < 4$$ | $$\displaystyle \frac{3}{6}$$ |
| $$1\leq x < 5$$ | $$\displaystyle \frac{4}{6}$$ |
| $$1\leq x < 6$$ | $$\displaystyle \frac{5}{6}$$ |
| $$x \leq 6$$ | $$1$$ |
El valor de la función distribución en $$-\infty$$ siempre será $$0$$, mientras que el valor en $$+\infty$$ siempre será $$1$$.
Esto resulta lógico, ya que la probabilidad de que el valor de $$x$$ sea más pequeño que $$-\infty$$ es nula, y la probabilidad de que tenga un valor menor que $$+\infty$$ es $$1$$ (ya que siempre es menor o igual a $$+\infty$$).
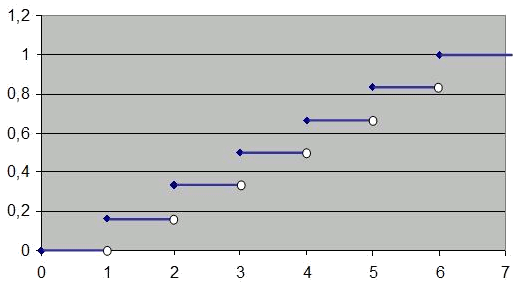
Al tratarse de una variable aleatoria discreta, la función distribución tendrá tramos planos. La probabilidad de que el resultado del dado sea inferior a $$5,2$$ es la misma a la de que sea inferior a $$5,3$$ o $$5,9$$.
