La funció distribució

La funció distribució d'una variable aleatòria $X$ és una funció que proporciona, en cada punt, la probabilitat acumulada fins aquest valor. És a dir:

$F (X) = p (X \leq x)$

Exemple

Per exemple, s'estudia la funció distribució de la variable aleatòria $X$ , resultat de tirar un dau perfecte.

La següent taula mostra els valors de $F (x)$ :

x	F (x)
$x < 1$	$0$
$1 \leq x < 2$	$\frac{1}{6}$
$1 \leq x < 3$	$\frac{2}{6}$
$1 \leq x < 4$	$\frac{3}{6}$
$1 \leq x < 5$	$\frac{4}{6}$
$1 \leq x < 6$	$\frac{5}{6}$
$x \leq 6$	$1$

El valor de la funció distribució en $- \infty$ sempre serà $0$ , mentre que el valor en $+ \infty$ sempre serà $1$ .

Això resulta lògic, ja que la probabilitat que el valor de $x$ sigui més petit que $- \infty$ és nul·la, i la probabilitat que tingui un valor menor que $+ \infty$ és $1$ (ja que sempre és menor o igual a $+ \infty$ ).

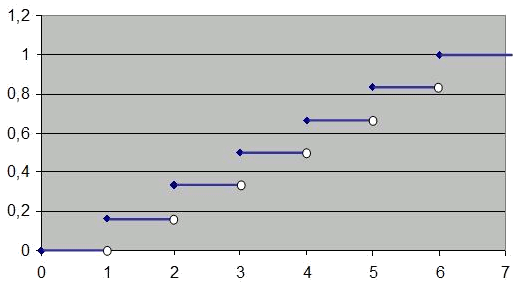
imagen

Com que es tracta d'una variable aleatòria discreta, la funció distribució tindrà trams plans. La probabilitat que el resultat del dau sigui inferior a $5, 2$ és la mateixa a la que sigui inferior a $5, 3$ o $5, 9$ .