Àrees de recintes al pla

Anem a introduir el càlcul de l'àrea en una regió del pla. Si anomenem a la regió del pla $D$, llavors:

$$\text{Àrea}(D)={\int }_{D}1dxdy$$

Es tracta doncs d'una integral doble. Per tant, l'únic que hem de fer és aconseguir parametritzar la regió $D$ per poder integrar. Tal com passa en càlcul d'integrals, de vegades ens resulta més còmode fer un canvi de variables, el més típic, a polars, per poder calcular l'àrea. En aquest cas, recordem que hem de multiplicar la funció que integrem pel determinant de la matriu jacobiana del canvi que estem utilitzant.

Calculem ara l'àrea d'un cercle de radi $R$. Suposarem que està centrada en l'origen, de manera que ve donat per l'equació: $x^2+y^2⩽R^2$.

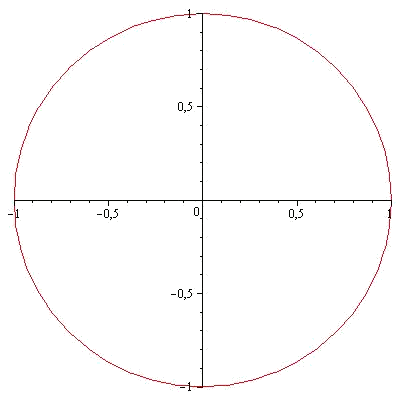
Aquesta regió es pot parametritzar utilitzant coordenades polars: $$\{\begin{array}{l}x=r\cos (\theta )\\ y=r\sin (\theta )\end{array}\text{ amb }r\in [0,R]\text{ i }\theta \in [0,2\pi ]$$

Hem de recordar de fer un canvi de variables suposa que hem de multiplicar la funció a integrar pel determinant de la matriu jacobiana del canvi, en aquest cas per $r$. Així:

$${\int }_0^R{\int }_0^{2\pi }1\cdot rd\theta dr$$