En aquest apartat calcularem àrees determinades per la gràfica d'una funció i l'eix de les $$x$$. Considerem una funció real $$f(x)$$ i la seva gràfica $$( x, f(x) )$$ en el pla:
.gif)
Volem calcular l'àrea acolorida $$A$$. És a dir, l'àrea, $$A$$, determinada per la gràfica de la funció, un cert interval $$[a, b]$$ i l'eix de les $$x$$, és a dir:
$$$A=\int_{a}^b f(x) \ dx$$$
Calculem l'àrea sota la funció $$f(x)=x^2$$ en l'interval $$[-2,2]$$. Representem la funció per tenir una noció geomètrica del problema:
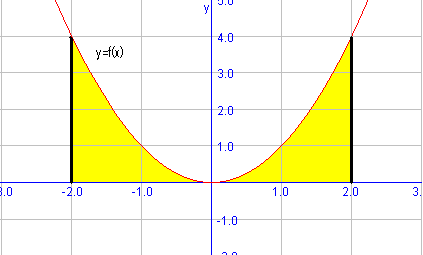
Hem d'integrar la funció en l'interval que delimita l'àrea, és a dir: $$$A=\int_{-2}^2 x^2 \ dx=\Big[ \dfrac{x^3}{3} \Big]_{-2}^2= \dfrac{2^3}{3}-\dfrac{(-2)^3}{3}=\dfrac{8}{3}-\dfrac{-8}{3}= \dfrac{16}{3}\mathrm{u}^2$$$
Nota: Quan escrivim $$u^2$$ ens referim a les unitats de superfície.
Calculem l'àrea sota la funció $$f(x)=\sqrt{x}+\sin x$$ en l'interval $$[0,4]$$. Tal com hem fet en l'exemple anterior, dibuixem primer la funció:
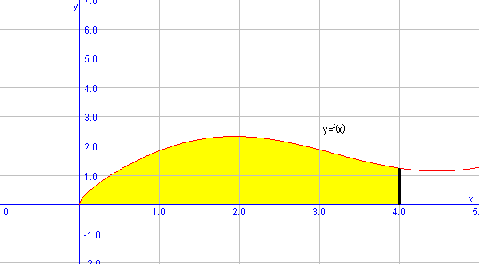
Per calcular l'àrea sota $$f(x)$$, hem d'integrar aquesta funció en l'interval corresponent: $$$ \begin{array}{rl} A=&\int_0^4(\sqrt{x}+\sin (x)) \ dx= \int_0^4\sqrt{x} \ dx + \int_0^4\sin(x) \ dx \\ =& \left[ \dfrac{x^{\frac{3}{2}}}{\dfrac{3}{2}} \right]_0^4+ [-\cos(x)]_0^4= \dfrac{2}{3}(8-0)-\cos(4)+1 \\ =& \dfrac{16}{3}+1.65=6.98 u^2 \end{array}$$$