Continuïtat d'una funció en un punt

De funcions n'hi ha de molts tipus i formes: funcions periòdiques, definides a trossos, creixents, decreixents, còncaves, convexes,... però entre totes elles, les podem classificar en dos conjunts més elementals: funcions contínues i funcions no contínues.

Vulgarment es diu que una funció és contínua si és possible dibuixar sense tenir necessitat d'aixecar el llapis del paper i per tant, dibuixar amb un sol traçat.

Matemàticament la definició és una mica més elaborada.

Considerem una funció $f (x)$ . Direm que es continua en el punt $x = a$ si es compleix que els límits laterals de $f (x)$ a $x = a$ coincideixen amb el valor de la funció en $x = a$ : $lim_{x \to a^{+}} f (x) = lim_{x \to a^{-}} f (x) = f (a)$ En la següent gràfica observem una funció contínua.

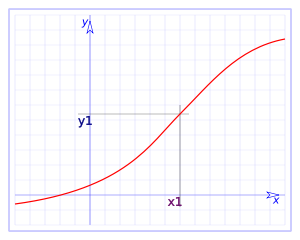
imagen

i podem veure que els límits laterals coincidiran amb el valor de la funció en el punt $x 1$ , $f (x 1) = y 1$ .

Vegem alguns exemples:

Exemple

Prenem la funció $f (x) = e^{- x^{2}}$ i mirem la continuïtat de la funció en el punt $x = 0$ : $\begin{array}{l} lim_{x \to 0^{+}} f (x) = lim_{x \to 0^{+}} e^{- x^{2}} = e^{0} = 1 \\ lim_{x \to 0^{-}} f (x) = lim_{x \to 0^{-}} e^{- x^{2}} = e^{0} = 1 \end{array}$ i com que els límits coincideixen amb el valor de la funció en el zero: $f (0) = e^{0} = 1$ , aleshores la funció és contínua en el zero.

Exemple

Per veure un exemple de funció no contínua en un punt, prenguem la funció $f (x) = {\begin{array}{rcl} x & si & x \neq 2 \\ 0 & si & x = 2 \end{array}$ , i mirem la continuïtat en $x$ =2. Llavors observem que: $\begin{array}{l} lim_{x \to 2^{+}} f (x) = lim_{x \to 2^{+}} x = 2 \\ lim_{x \to 2^{-}} f (x) = lim_{x \to 2^{-}} x = 2 \end{array}$ i si avaluem la funció en $x = 2$ tenim que $f (2) = 0$ , de manera que la funció no és contínua en el punt $x = 2$ .