Continuidad de una función en un punto

Funciones hay de muchos tipos y formas: funciones periódicas, definidas a trozos, crecientes, decrecientes, cóncavas, convexas, ... Pero entre todas ellas, las podemos clasificar en dos conjuntos más elementales: funciones continuas y funciones no continuas.

Vulgarmente se dice que una función es continua si es posible dibujarla sin tener necesidad de levantar el lápiz del papel y por lo tanto, dibujarla con un solo trazado.

Matemáticamente la definición es un poco más elaborada.

Consideremos una función $f (x)$ . Diremos que es continua en el punto $x = a$ si se cumple que los límites laterales de $f (x)$ en $x = a$ coinciden con el valor de la función en $x = a$ : $lim_{x \to a^{+}} f (x) = lim_{x \to a^{-}} f (x) = f (a)$ En la siguiente gráfica observamos una función continua.

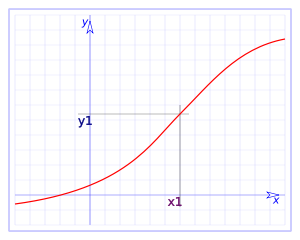
imagen

y podemos ver que los límites laterales coincidirán con el valor de la función en el punto $x 1$ , $f (x 1) = y 1$ .

Veamos algunos ejemplos:

Ejemplo

Tomamos la función $f (x) = e^{- x^{2}}$ y miremos la continuidad de la función en el punto $x = 0$ : $\begin{array}{l} lim_{x \to 0^{+}} f (x) = lim_{x \to 0^{+}} e^{- x^{2}} = e^{0} = 1 \\ lim_{x \to 0^{-}} f (x) = lim_{x \to 0^{-}} e^{- x^{2}} = e^{0} = 1 \end{array}$ y como los límites coinciden con el valor de la función en el cero: $f (0) = e^{0} = 1$ , entonces la función es continua en el cero.

Ejemplo

Para ver un ejemplo de función no continua en un punto, tomemos la función $f (x) = {\begin{array}{rcl} x & si & x \neq 2 \\ 0 & si & x = 2 \end{array}$ , y miremos la continuidad en $x$ =2. Entonces observamos que: $\begin{array}{l} lim_{x \to 2^{+}} f (x) = lim_{x \to 2^{+}} x = 2 \\ lim_{x \to 2^{-}} f (x) = lim_{x \to 2^{-}} x = 2 \end{array}$ y si evaluamos la función en $x = 2$ tenemos que $f (2) = 0$ , por lo que la función no es continua en el punto $x = 2$ .