De una manera menos estricta podemos definir la continuidad lateral, por la izquierda y por la derecha.
Una función es continua en el punto $$x=a$$ por la derecha si: $$$\displaystyle \lim_{x \to a^+}f(x)=f(a)$$$ y decimos que es continua en el punto $$x=a$$ por la izquierda si: $$$\displaystyle \lim_{x \to a^-}f(x)=f(a)$$$ Podemos ver a continuación un ejemplo de función continua por la izquierda pero no por la derecha en el punto $$x=1$$
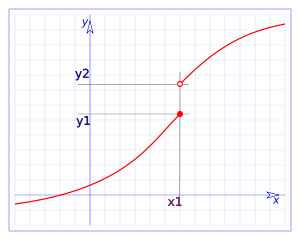
Veamos unos ejemplos para entender mejor el concepto:
Tomemos la función $$\displaystyle f(x)=\left\{\begin{array}{rcl} x & \mbox{ si } & x < 1 \\ -x & \mbox{ si } & x \geq 1 \end{array}\right.$$ y estudiemos la continuidad lateral en $$x=1$$:
Continuidad lateral por la derecha: $$$\displaystyle \lim_{x \to 1^+}f(x)=\lim_{x \to 1} -x= -1$$$ y la función en $$x=1$$ vale $$f(1)=-1$$, por lo que la función es continua por la derecha.
Continuidad lateral por la izquierda: $$$\displaystyle \lim_{x \to 1^-} f(x)=\lim_{x \to 1} x=1$$$ y la función en $$x=1$$ vale $$f(1)=-1$$, por lo que la función no es continua por la izquierda.
Observamos que las funciones que son continuas en un punto, son continuas por la derecha y por la izquierda, o dicho al revés, que cuando la continuidad lateral coincide por la derecha y por la izquierda, decimos que la función es continua en el punto.
