Continuïtat lateral

D'una manera menys estricta podem definir la continuïtat lateral, per l'esquerra i per la dreta.

Una funció és contínua en el punt $x = a$ per la dreta si: $lim_{x \to a^{+}} f (x) = f (a)$ i diem que és contínua en el punt $x = a$ per l'esquerra si: $lim_{x \to a^{-}} f (x) = f (a)$ Podem veure a continuació un exemple de funció contínua per l'esquerra però no per la dreta en el punt $x = 1$

imagen

Vegem uns exemples per entendre millor el concepte:

Exemple

Prenguem la funció $f (x) = {\begin{array}{rcl} x & si & x < 1 \\ - x & si & x \geq 1 \end{array}$ i estudiem la continuïtat lateral en $x = 1$ :

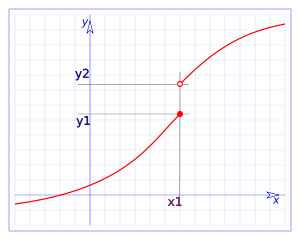
Continuïtat lateral per la dreta: $lim_{x \to 1^{+}} f (x) = lim_{x \to 1} - x = - 1$ i la funció en $x = 1$ val $f (1) = - 1$ , de manera que la funció és contínua per la dreta.

Continuïtat lateral per l'esquerra: $lim_{x \to 1^{-}} f (x) = lim_{x \to 1} x = 1$ i la funció en $x = 1$ val $f (1) = - 1$ , de manera que la funció no és contínua per l'esquerra.

Observem que les funcions que són contínues en un punt, són contínues per la dreta i per l'esquerra, o dit al revés, que quan la continuïtat lateral coincideix per la dreta i per l'esquerra, diem que la funció és contínua en el punt.