Derivades parcials

Sabem que la derivada d'una funció d'una variable en un punt ens dóna el pendent de la recta tangent a la funció en aquest punt. Això vol dir que sabem la rapidesa de creixement/decreixement de la funció en aquest punt.

imagen

Ara suposem que tenim una funció $f$ que depèn de més d'una variable, per exemple $f (x, y) = - x^{2} + 2 x y - y$ .

En ser una funció de dues variables, la gràfica és una superfície, i per tant hi ha infinites direccions entre les que podem estudiar el creixement.

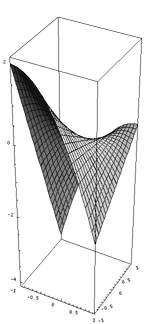
imagen

Doncs bé, les derivades parcials ens indicaran també el pendent d'una recta concreta tangent a la superfície. Abans, però, aprendrem a calcular derivades parcials, ja que és un metodologia a la que després donarem sentit.

Per calcular una derivada parcial d'una funció en diverses variables, hem de derivar com sempre respecte una de les variables i mantenir les altres com a constants, (com a valors fixos).

En el nostre exemple $f (x, y) = - x^{2} + 2 x y - y$ , si volem fer la derivada parcial respecte $x$ , considerem la variable $y$ com una constant, "un nombre", i el que queda serà com derivar una funció d'una variable, $f (x)$ . Vegem-ho:

Exemple

$- x^{2}$ només depèn de $x$ ; per tant, la seva derivada és $- 2 x$ .

$2 x y$ conté la variable $y$ , però és como si fos una constant, un nombre. Si fos un $3$ faríem $2 x 3 = 6 x$ , i la derivada seria $6$ . Doncs ara escric $2 x y$ com a $2 y x$ i considero $2 y$ com si fos el $6$ . Per tant, la derivada de $2 x y = 2 y x$ és $2 y$ .

I finalment, $y$ no conté la variable $x$ , i la derivada d'una constant és $0$ . Per tant, desapareix.

Ara només ens falta saber la notació per poder escriure-ho matemàticament. Per a la derivada parcial d'una funció $f$ respecte la variable $x$ , podem trobar les notacions:

$\frac{δ f}{δ x}$ $δ_{x} f$ $f_{x}$

Exemple

Així, la nostra derivada parcial respecte $x$ de $f (x, y) = - x^{2} + 2 x y - y$ s'escriu

$\frac{δ f}{δ x} = - 2 x + 2 y - 0 = 2 x + 2 y$ $δ_{x} f = - 2 x + 2 y$ $f_{x} = - 2 x + 2 y$

I ara us preguntareu: També podem fer la derivada parcial respecte $y$ , no? Doncs clar que sí.

Fem el càlcul de $\frac{δ f}{δ y}$ , amb el qual ens imaginem que $x$ és una constant.

Exemple

$- x^{2}$ no conté la variable $y$ , i com abans, és com si tinguéssim simplement una constant. La seva derivada és $0$ .

$2 x y$ conté la variable $x$ , però és com si fos una constant, un nombre. Per tant, la derivada de $2 x y$ és $2 x$ .

I finalment, com que estem derivant respecte $y$ , la derivada de $y$ és $1$ .

Així, $\frac{δ f}{δ y} = δ_{y} f = f_{y} = 2 x - 1$

Interpretació geomètrica de la derivada parcial

Però què significa geomètricament el càlcul d'una derivada parcial? Vegem el següent exemple:

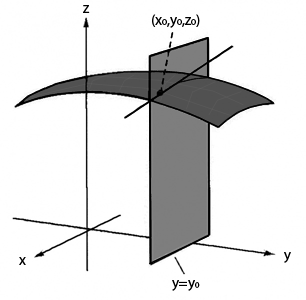
imagen

En aquest gràfic tenim una superfície $z = f (x, y)$ de la qual estem fent la derivada parcial respecte la variable $x$ en un punt $x_{0}, y_{0}, z_{0}$ . Hem vist que fer la parcial respecte $x$ significa deixar la variable $y$ com a constant. Mantenir el valor fix $y = y_{0}$ ens dóna com a resultat un pla que passa pel punt $y_{0}$ . Construïm llavors el pla que sigui paral·lel a l'eix $x$ . Aquest pla talla la nostra superfície. A la corba intersecció considerem la recta tangent en el punt $x_{0}, y_{0}, z_{0}$ . La derivada parcial ens donarà el pendent d'aquesta recta.

Exemple

Si en la nostra funció d'exemple $f (x, y) = - x^{2} + 2 x y - y$ volem el valor del pendent de la recta tangent a la superfície en el punt $3, 1$ en la direcció de l'eix $x$ , ens queda

$\frac{δ f}{δ x} = - 2 x + 2 y$ $\frac{δ f (3, 1)}{δ x} = (- 2) \cdot 3 + 2 \cdot 1 = - 6 + 2 = - 4$

En una funció $z = f (x, y)$ , la derivada parcial respecte $y$ es representaria gràficament seguint l'exemple gràfic:

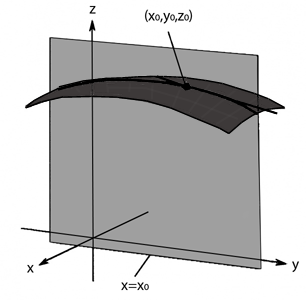
imagen

Ara el valor constant és $x = x_{0}$ , i el pla és paral·lel a l'eix $y$ .

Exemple

En la nostra funció d'exemple, si volem saber el pendent en la direcció $y$ en el punt $(0, 1)$ , obtenim

$\frac{δ f}{δ y} = 2 x - 1$ $\frac{δ f (0, 1)}{δ y} = - 1$

i veiem que la inclinació de la superfície en aquest punt i en la direcció ja comentada és descendent.

En definitiva, que quan calculem les derivades parcials $\frac{δ f}{δ x}$ o $\frac{δ f}{δ y}$ en el punt $x_{0}, y_{0}, z_{0}$ , el valor que obtenim és el pendent de la superfície en la direcció de l'eix $x$ o de l'eix $y$ , respectivament.

Definició formal de derivada parcial

La definició formal de derivada parcial segueix sent el càlcul d'un límit, com amb la derivada d'una funció d'una variable.

Sigui $U$ un subconjunt obert de $R^{n}$ i una funció $f : U \to R$ . Definim la derivada parcial de $f$ en el punt $p \in U$ , $p = p_{1}, . . ., p_{n}$ , respecte la variable $x_{i}$ com a

$\frac{δ f (p)}{δ x_{i}} = lim_{h \to 0} \frac{f (p_{1}, . . ., p_{i - 1}, p_{i} + h, p_{i + 1}, . . ., p_{n}) - f (p_{1}, . . ., p_{n})}{h}$

Exemples de càlcul de derivades parcials

Per a una bona realització s'han de tenir presents dues coses: les regles de derivació en una variable i saber imaginar-nos com a constants les variables que corresponguin en cada cas. Veuràs com és qüestió de pràctica.

Exemple

Donada la funció $f (x, y) = \sqrt{x^{3} + y^{2}}$ , calcula $f_{x} (1, 1)$ .

Reescric $f (x, y) = (x^{3} + y^{2})^{\frac{1}{2}}$ com ho fèiem per derivar arrels quan només hi havia una variable. Ara pensem en $y$ com una constant i derivem fent servir les regles habituals:

$f_{x} = \frac{1}{2} (x^{3} + y^{2})^{- \frac{1}{2}} \cdot 3 x^{2} = \frac{3 x^{2}}{2 \sqrt{x^{3} + y^{2}}}$

Per saber el pendent en el punt $(1, 1)$ , substituïm

$f_{x} (1, 1) = \frac{3}{2 \sqrt{2}}$

Exemple

Donada la funció $f (x, y) = \frac{2 x y - y}{x^{2} + y}$ , calcula la derivada parcial respecte $x$ i $y$ .

$\frac{δ f}{δ x} = \frac{2 y (x^{2} + y) - (2 x y - y) 2 x}{(x^{2} + y)^{2}} = \frac{2 y x^{2} + 2 y^{2} - 4 x^{2} y + 2 x y}{(x^{2} + y)^{2}} = \frac{- 2 x^{2} y + 2 x y + 2 y^{2}}{(x^{2} + y)^{2}} = \frac{2 (- x^{2} y + x y + y^{2})}{(x^{2} + y)^{2}}$

$\frac{δ f}{δ y} = \frac{(2 x - 1) (x^{2} + y) - (2 x y - y)}{(x^{2} + y)^{2}} = \frac{2 x^{3} + 2 x y - x^{2} - y - 2 x y + y}{(x^{2} + y)^{2}} = \frac{2 x^{3} - x^{2}}{(x^{2} + y)^{2}}$

Exemple

Donada la funció $f (x, y, z) = x^{2} y^{3} - 2 x y z^{3}$ , calcula el pendent de la recta tangent al punt $(1, - 1, 1)$ en les direccions dels eixos $x$ , $y$ i $z$ .

$\frac{δ f}{δ x} = 2 x y^{3} - 2 y z^{3}$ $\frac{δ f (1, - 1, 1)}{δ x} = 2 \cdot 1 \cdot (- 1)^{3} - 2 \cdot (- 1) \cdot 1^{3} = 0$

$\frac{δ f}{δ y} = 3 x^{2} y^{2} - 2 x z^{3}$ $\frac{δ f (1, - 1, 1)}{δ y} = 3 - 2 = 1$

$\frac{δ f}{δ z} = - 6 x y z^{2}$ $\frac{δ f (1, - 1, 1)}{δ z} = 6$

Exemple

Donada la funció $f (x, y, z) = \frac{2 z}{y + \sin (x)}$ calcula les derivades parcials respecte $x$ , $y$ i $z$ .

$\frac{δ f}{δ x} = \frac{- 2 z \cos (x)}{(y + \sin (x))^{2}}$

$\frac{δ f}{δ y} = \frac{- 2 z}{(y + \sin (x))^{2}}$

$\frac{δ f}{δ z} = \frac{2 (y + \sin (x)) - 2 z \cdot 0}{(y + \sin (x))^{2}} = \frac{2 (y + \sin (x))}{(y + \sin (x))^{2}} = \frac{2}{y + \sin (x)}$

Més aplicacions de la derivada parcial

Arribats en aquest punt, potser has pensat en alguna altra informació que podrien proporcionar les derivades parcials. I és que també podem interpretar que la derivada parcial mesura la rapidesa de canvi de la variable que derivem respecte a la variable que deixem fixa. Així podem mesurar com canvia $y$ quan deixem $x$ fixa i al revés. Vegem un exemple.

Exemple

Imaginem una placa solar rectangular tal que en zones diferents absorbeix quantitats diferents de llum solar i per tant cada cèl·lula produeix una quantitat diferent d'energia. Tenim una relació tal que, en un punt $(x, y)$ de la placa, la potència d'energia generada la podem deduir amb la relació $E (x, y) = \frac{3}{10} x y + y$

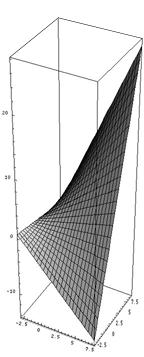
imagen

Les unitats de $x$ i $y$ són centímetres i la potència d'energia $E$ es mesura en watts. ¿Com varia la potència energètica $E$ en el centre de la placa, $(65, 120)$ , quan $x$ roman fixa en els $65$ cm?

Per saber-ho hem de calcular $E_{y} (65, 120)$ . $E_{y} = \frac{3}{10} x + 1 \Rightarrow E_{y} (65, 120) = 20, 5$

Així sabem que situats sobre el punt $x = 65$ , $y = 120$ la potència energètica augmenta a mesura que avancem en la direcció de l'eix $y$ , ja que la derivada parcial en aquesta direcció és positiva. A més, la potència energètica generada augmentarà amb una rapidesa de $20, 5$ W.