Sabemos que la derivada de una función de una variable en un punto nos da la pendiente de la recta tangente a la función en ese punto. Esto significa que sabemos la rapidez de crecimiento/decrecimiento de la función en ese punto.
Ahora supongamos que tenemos una función $$f$$ que depende de más de una variable, por ejemplo $$f(x,y)=-x^2+2xy-y$$.
Al ser una función de dos variables la gráfica es una superficie, y entonces hay infinitas direcciones entre las que estudiar el crecimiento.
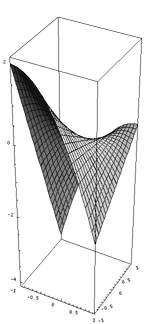
Pues bien, las derivadas parciales nos indicarán también la pendiente de una recta concreta tangente a la superficie. Antes, pero, vamos a aprender a calcular derivadas parciales, ya que es un metodologia a la que luego le daremos sentido.
Para calcular una derivada parcial de una función en diversas variables tenemos que derivar como siempre respecto una de las variables y mantener las demás como constantes, (como valores fijos).
En nuestro ejemplo $$f(x,y)=-x^2+2xy-y$$, si queremos hacer la derivada parcial respecto $$x$$, consideramos la variable $$y$$ como una constante, "un número", y entonces nos queda como derivar una función de una variable, $$f(x)$$. Veamos:
$$-x^2$$ sólo depende de $$x$$, por lo tanto su derivada es $$-2x$$.
$$2xy$$ contiene la variable $$y$$, pero es como si fuera una constante, un número. Si fuera un $$3$$ haríamos $$2x3=6x$$ y la derivada sería $$6$$. Pues ahora escribo $$2xy$$ como $$2yx$$ y considero $$2y$$ como si fuera el $$6$$. Por lo tanto la derivada de $$2xy=2yx$$ es $$2y$$.
Y finalmente, $$y$$ no contiene la variable $$x$$, y la derivada de una constante es $$0$$, con lo que desaparece.
Ahora sólo nos falta saber la notación para poder escribirlo correcto matemáticamente. Para la derivada parcial de una función $$f$$ respecto la variable $$x$$ podemos encontrarnos las notaciones:
$$$\dfrac{\delta f}{\delta x}$$$ $$$\delta_x f$$$ $$$f_x$$$
Así, nuestra derivada parcial respecto $$x$$ de $$f(x,y)=-x^2+2xy-y$$ se escribe
$$$\dfrac{\delta f}{\delta x}=-2x+2y-0=2x+2y$$$ $$$\delta_x f=-2x+2y$$$ $$$f_x=-2x+2y$$$
Y ahora os preguntaréis, ¿también podemos hacer la derivada parcial respecto $$y$$ no? Pues claro.
Hacemos el cálculo de $$\dfrac{\delta f}{\delta y}$$, con lo cual nos imaginamos que $$x$$ es una constante.
$$-x^2$$ no contiene la variable $$y$$, y como entonces es como si tuviéramos simplemente una constante, su derivada es $$0$$.
$$2xy$$ contiene la variable $$x$$, pero es como si fuera una constante, un número. Por lo tanto la derivada de $$2xy$$ es $$2x$$.
Y finalmente, como estamos derivando respecto $$y$$, la derivada de $$y$$ es $$1$$.
Así $$$\dfrac{\delta f}{\delta y}=\delta_y f=f_y=2x-1$$$
Interpretación geométrica de la derivada parcial
¿Pero qué es lo que significa geométricamente el cálculo de una derivada parcial? Veamos el siguiente ejemplo:
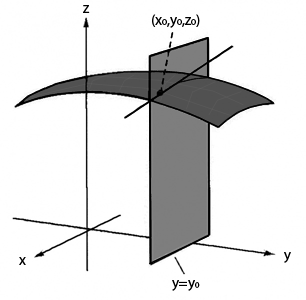
En este gráfico tenemos una superficie $$z=f(x,y)$$ de la cual estamos haciendo la derivada parcial respecto la variable $$x$$ en un punto $$x_0,y_0,z_0$$. Hemos visto que hacer la parcial respecto $$x$$ significa dejar la variable $$y$$ como constante. Mantener el valor fijo $$y=y_0$$ nos da como resultado un plano que pasa por el punto $$y_0$$. Construimos entonces el plano que sea paralelo al eje $$x$$. Este plano corta nuestra superfície. En la curva intersección consideramos la recta tangente en el punto $$x_0,y_0,z_0$$. La derivada parcial nos dará la pendiente de esta recta.
Si en nuestra función de ejemplo $$f(x,y)=-x^2+2xy-y$$ queremos el valor de la pendiente de la recta tangente a la superficie en el punto $$3,1$$ en la dirección del eje $$x$$ nos queda
$$$\dfrac{\delta f}{\delta x}=-2x+2y$$$ $$$\dfrac{\delta f(3,1)}{\delta x}=(-2)·3+2·1=-6+2=-4$$$
En una función $$z=f(x,y)$$, la derivada parcial respecto $$y$$ se representaría gráficamente siguiendo el ejemplo gráfico:
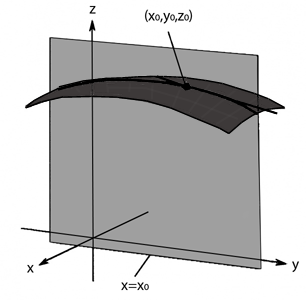
Ahora el valor constante es $$x=x_0$$ y el plano es paralelo al eje $$y$$.
En nuestra función de ejemplo, si queremos saber la pendiente en la dirección $$y$$ en el punto $$(0,1)$$ obtenemos
$$$\dfrac{\delta f}{\delta y}=2x-1$$$ $$$\dfrac{\delta f(0,1)}{\delta y}=-1$$$
con lo que la inclinación de la superfície en este punto y en la dirección ya comentada es descendiente.
En definitiva, que cuando calculamos las derivadas parciales $$\dfrac{\delta f}{\delta x}$$ y $$\dfrac{\delta f}{\delta y}$$ en el punto $$x_0,y_0,z_0$$ el valor que obtenemos es la pendiente de la superficie en la dirección del eje $$x$$ o del eje $$y$$, respectivamente.
Definición formal de derivada parcial
La definición formal de derivada parcial sigue siendo el cálculo de un límite, como la derivada de una función de una variable.
Sea $$U$$ un subconjunto abierto de $$\mathbb{R}^n$$ y una función $$f: \ U \rightarrow R$$. Definimos la derivada parcial de $$f$$ en el punto $$p\in U$$, $$p=p_1,...,p_n$$, respecto la variable $$x_i$$ como
$$$\dfrac{\delta f(p)}{\delta x_i}=\lim_{h\rightarrow 0}\dfrac{f(p_1,...,p_{i-1},p_i+h,p_{i+1},...,p_n)-f(p_1,...,p_n)}{h}$$$
Ejemplos de cálculo de derivadas parciales
Para una buena realización hay que tener en mente dos cosas: las reglas de derivación en una variable y saber imaginarnos las variables que correspondan en cada caso como constantes. Verás como es cuestión de práctica.
Dada la función $$f(x,y)=\sqrt{x^3+y^2}$$ calcula $$f_x(1,1)$$.
Reescribo $$f(x,y)=(x^3+y^2)^{\frac{1}{2}}$$ como lo hacíamos para derivar raíces cuando había solamente una variable. Ahora pensamos en $$y$$ como una constante y derivamos usando las reglas habituales
$$$f_x=\dfrac{1}{2}(x^3+y^2)^{-\frac{1}{2}}\cdot3x^2=\dfrac{3x^2}{2\sqrt{x^3+y^2}}$$$
Para saber la pendiente en el punto $$(1,1)$$ sustituimos
$$$f_x (1,1)=\dfrac{3}{2\sqrt{2}}$$$
Dada la función $$f(x,y)=\dfrac{2xy-y}{x^2+y}$$ calcula la derivada parcial respecto $$x$$ e $$y$$.
$$$\dfrac{\delta f}{\delta x}=\dfrac{2y(x^2+y)-(2xy-y)2x}{(x^2+y)^2}=\dfrac{2yx^2+2y^2-4x^2y+2xy}{(x^2+y)^2}=\dfrac{-2x^2y+2xy+2y^2}{(x^2+y)^2}=\dfrac{2(-x^2y+xy+y^2)}{(x^2+y)^2}$$$
$$$\dfrac{\delta f}{\delta y}=\dfrac{(2x-1)(x^2+y)-(2xy-y)}{(x^2+y)^2}=\dfrac{2x^3+2xy-x^2-y-2xy+y}{(x^2+y)^2}=\dfrac{2x^3-x^2}{(x^2+y)^2}$$$
Dada la función $$f(x,y,z)=x^2y^3-2xyz^3$$ calcula la pendiente de la recta tangente al punto $$(1,-1,1)$$ en las direcciones de los ejes $$x$$, $$y$$ e $$z$$.
$$$\dfrac{\delta f}{\delta x}=2xy^3-2yz^3$$$ $$$\dfrac{\delta f(1,-1,1)}{\delta x}=2\cdot1\cdot(-1)^3-2\cdot(-1)\cdot1^3=0$$$
$$$\dfrac{\delta f}{\delta y}=3x^2y^2-2xz^3$$$ $$$\dfrac{\delta f(1,-1,1)}{\delta y}=3-2=1$$$
$$$\dfrac{\delta f}{\delta z}=-6xyz^2$$$ $$$\dfrac{\delta f(1,-1,1)}{\delta z}=6$$$
Dada la función $$f(x,y,z)=\dfrac{2z}{y+\sin(x)}$$ calcula las derivadas parciales respecto $$x$$, $$y$$ e $$z$$.
$$$\dfrac{\delta f}{\delta x}=\dfrac{-2z\cos(x)}{(y+\sin(x))^2}$$$
$$$\dfrac{\delta f}{\delta y}=\dfrac{-2z}{(y+\sin(x))^2}$$$
$$$\dfrac{\delta f}{\delta z}=\dfrac{2(y+\sin(x))-2z\cdot0}{(y+\sin(x))^2}=\dfrac{2(y+\sin(x))}{(y+\sin(x))^2}=\dfrac{2}{y+\sin(x)}$$$
Más aplicaciones de la derivada parcial
Llegados a este punto a lo mejor has pensado en otra información que podrían proporcionar las derivadas parciales. Y es que también podemos interpretar que la derivada parcial mide la rapidez de cambio de la variable que derivamos respecto a la variable que dejamos fija. Así podemos medir como cambia $$y$$ cuando dejamos $$x$$ fija y al revés. Veamos un ejemplo.
Imaginemos una placa solar rectangular tal que en zonas distintas absorbe cantidades diferentes de luz solar y por lo tanto cada celda produce una cantidad distinta de energía. Tenemos una relación tal que en un punto $$(x,y)$$ de la placa la potencia de energía generada la podemos deducir con la relación $$$E(x,y)= \dfrac{3}{10}xy + y$$$
Las unidades de $$x$$ e $$y$$ son centímetros y la potencia de energía $$E$$ en Watts. ¿Cómo varía la potencia energética $$E$$ en el centro de la placa, $$(65,120)$$, cuando $$x$$ permanece fija en los $$65$$ cm?
Para saberlo tenemos que calcular $$E_y(65,120)$$. $$$E_y=\dfrac{3}{10}x+1 \Rightarrow E_y(65,120)=20,5$$$
Así sabemos que situados sobre el punto $$x=65$$, $$y=120$$ la potencia energética aumenta a medida que avanzamos en la dirección del eje $$y$$ ya que la derivada parcial en esta dirección es positiva. Además la potencia energética generada aumentará con una rapidez de $$20,5$$ W.

