Divisors d'un nombre
Si es pensa en dos nombres enters qualssevol, per exemple, $$12$$ i $$3$$, es pot fer la seva divisió:
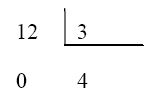
Per a més comoditat s'utilitzarà el format de taules per representar les divisions:
|
$$12$$ |
$$3$$ |
|
$$0$$ |
$$4$$ |
Obtenint com a resultat el número $$4$$, un altre nombre enter. D'això se'n diu una divisió exacta, ja que el residu de la divisió és $$0$$.
Ara, si es pensa en dos nombres, per exemple, $$12$$ i $$5$$, es veurà que també es poden dividir:
|
$$12$$ |
$$5$$ |
|
$$2$$ |
$$2$$ |
En aquest cas, obtenim com a residu $$2$$. Per tant, no serà una divisió exacta.
Si es prova a dividir diferents nombres entre si es comprovarà que en alguns casos s'obtenen divisions exactes i en altres no.
Si es divideix el número $$12$$ entre $$1, 2, 3, 4, 6$$ o $$12$$, s'obtenen resultats exactes, amb el residu $$0$$. $$$\begin{array}{l} 12\div 1=12 \\ 12 \div 2=6 \\ 12 \div 3=4 \\ 12\div 4= 3 \\ 12\div 6=2 \\ 12 \div 12=1\end{array}$$$ Es diu que els números $$1, 2, 3, 4, 6$$ i $$12$$ són divisors del nombre $$12$$.
De manera que es pot dir que un nombre és divisor d'un altre quan la divisió del segon entre el primer (el divisor) és una divisió exacta.
Els divisors del nombre $$10$$ són $$1, 2, 5$$ i $$10$$. $$$10 \div 1 = 10 \\ 10 \div 2 = 5 \\ 10 \div 5 = 2 \\10 \div 10 = 1$$$
Els divisors del nombre $$27$$ són $$1, 3, 9$$ i $$27$$.$$$21 \div 1=27 \\ 27 \div 3=9 \\ 27 \div 9 = 3 \\ 27 \div 27 =1$$$
Els divisors del nombre $$35$$ són $$1, 5, 7$$ i $$35$$.$$$35 \div 1=35 \\ 35 \div 5= 7 \\ 35 \div 7=5 \\35 \div 35 =1$$$
Els divisors del nombre $$40$$ són $$1, 2, 4, 5, 8, 10, 20$$ i $$40$$. $$$40 \div 1 = 40 \\ 40 \div 2 = 20 \\40 \div 4 =10\\40 \div 5= 8 \\40 \div 8 = 5 \\ 40 \div 10=4 \\ 40 \div 20 =2 \\40 \div 40=1$$$
Com es veu en els exemples, els divisors d'un nombre sempre seran menors que ell. Entre ells estarà sempre l'$$1$$, pel que pot ser dividit de forma exacta qualsevol nombre.
A més, qualsevol nombre serà sempre divisor de si mateix, donant com a quocient l'$$1$$.
Múltiples d'un nombre
Si es pren un dels exemples anteriors, per exemple el número $$35$$, es pot concloure que $$35$$ és un múltiple de qualsevol dels seus divisors, que són $$1, 5, 7$$ i $$35$$.
Un nombre és múltiple d'un altre quan aquest últim pot multiplicar per un tercer número per obtenir el primer.
En aquest cas, es pot dir, per exemple, que $$35$$ és múltiple de $$5$$ perquè:
$$5 \times 7=35$$
De la mateixa manera, $$35$$ és múltiple de $$7$$ per la mateixa raó.
En els altres exemples, i portant a terme les multiplicacions entre divisors que donen lloc al nombre del qual hem partit, ja sigui $$12, 10, 27$$ o $$40$$, podem concloure que:
$$12$$ és múltiple de $$1, 2, 3, 4, 6$$ i $$12$$ perquè tots aquests números poden ser multiplicats per un altre i donar lloc a $$12$$. $$$1 \times 12=12 \\ 2 \times 6 = 12 \\ 3 \times 4 =12 $$$ $$10$$ és múltiple de de $$1, 2, 5$$ i $$10$$. $$$1 \times 10 = 10 \\ 2 \times 5 = 10$$$ $$27$$ és múltiple de $$1, 3, 9$$ i $$27$$. $$$1 \times 27 = 27 \\ 3 \times 9 =27 $$$ $$40$$ és múltiple de $$1, 2, 4, 5, 8, 10, 20$$ i $$40$$. $$$1 \times 40=40 \\ 2\times 20=40 \\ 40\times 10=40 \\ 5\times 8=40$$$
Com es veu en els exemples, qualsevol nombre (diferent de zero) és múltiple de si mateix i de la unitat. A més, qualsevol nombre té infinits múltiples ja que sempre podrà ser multiplicat per un nombre qualsevol.