Divisores de un número
Si se piensa en dos números enteros cualesquiera, por ejemplo, $$12$$ y $$3$$, se puede hacer su división:
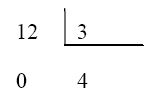
Para mayor comodidad se utilizará el formato de tablas para reprentar las divisiones:
|
$$12$$ |
$$3$$ |
|
$$0$$ |
$$4$$ |
Obteniendo como resultado el número $$4$$, otro número entero. A esto se le llama una división exacta, ya que el resto de la división es $$0$$.
Ahora, si se piensa en otros dos números, por ejemplo, $$12$$ y $$5$$, se verá que también se pueden dividir:
|
$$12$$ |
$$5$$ |
|
$$2$$ |
$$2$$ |
En este caso, obtenemos un resto, el número $$2$$. Por tanto, no será una división exacta.
Si se prueba a dividir diferentes números entre sí se comprobará que en algunos casos se obtienen divisiones exactas y en otros no.
Si se divide el número $$12$$ entre $$1, 2, 3, 4, 6$$ o $$12$$, se obtienen resultados exactos, con resto $$0$$. $$$\begin{array}{l} 12\div 1=12 \\ 12 \div 2=6 \\ 12 \div 3=4 \\ 12\div 4= 3 \\ 12\div 6=2 \\ 12 \div 12=1\end{array}$$$ Se dice que los números $$1, 2, 3, 4, 6$$ y $$12$$ son divisores del número $$12$$.
De manera que se puede decir que un número es divisor de otro cuando la división del segundo entre el primero (el divisor) es una división exacta.
Los divisores del número $$10$$ son $$1, 2, 5$$ y $$10$$. $$$10 \div 1 = 10 \\ 10 \div 2 = 5 \\ 10 \div 5 = 2 \\10 \div 10 = 1$$$
Los divisores del número $$27$$ son $$1, 3, 9$$ y $$27$$.$$$21 \div 1=27 \\ 27 \div 3=9 \\ 27 \div 9 = 3 \\ 27 \div 27 =1$$$
Los divisores del número $$35$$ son $$1, 5, 7$$ y $$35$$.$$$35 \div 1=35 \\ 35 \div 5= 7 \\ 35 \div 7=5 \\35 \div 35 =1$$$
Los divisores del número $$40$$ son $$1, 2, 4, 5, 8, 10, 20$$ y $$40$$. $$$40 \div 1 = 40 \\ 40 \div 2 = 20 \\40 \div 4 =10\\40 \div 5= 8 \\40 \div 8 = 5 \\ 40 \div 10=4 \\ 40 \div 20 =2 \\40 \div 40=1$$$
Como se ve en los ejemplos, los divisores de un número siempre serán menores que él. Entre ellos estará siempre el $$1$$, por el que puede ser dividido de forma exacta cualquier número. Además, cualquier número será siempre divisor de sí mismo, dando como cociente el $$1$$.
Múltiplos de un número
Si se toma uno de los ejemplos anteriores, por ejemplo el número $$35$$, se puede concluir que $$35$$ resulta un múltiplo de cualquiera de sus divisores, que son $$1, 5, 7$$ y $$35$$.
Un número es múltiplo de otro cuando éste último puede multiplicarse por un tercer número para obtener el primero.
En este caso, se puede decir, por ejemplo, que $$35$$ es múltiplo de $$5$$ porque:
$$5 \times 7=35$$
De la misma manera, $$35$$ es múltiplo de $$7$$ por la misma razón.
En los otros ejemplos, y llevando a cabo las multiplicaciones entre divisores que dan lugar al número del que hemos partido, ya sea $$12, 10, 27$$ o $$40$$, podemos concluir que:
$$12$$ es múltiplo de $$1, 2, 3, 4, 6$$ y $$12$$ porque todos estos números pueden ser multiplicados por otro y dar lugar a $$12$$. $$$1 \times 12=12 \\ 2 \times 6 = 12 \\ 3 \times 4 =12 $$$ $$10$$ es múltiplo de $$1, 2, 5$$ y $$10$$. $$$1 \times 10 = 10 \\ 2 \times 5 = 10$$$ $$27$$ es múltiplo de $$1, 3, 9$$ y $$27$$. $$$1 \times 27 = 27 \\ 3 \times 9 =27 $$$ $$40$$ es múltiplo de $$1, 2, 4, 5, 8, 10, 20$$ y $$40$$. $$$1 \times 40=40 \\ 2\times 20=40 \\ 40\times 10=40 \\ 5\times 8=40$$$
Como se ve en los ejemplos, cualquier número (distinto de cero) es múltiplo de sí mismo y de la unidad. Además, cualquier número tiene infinitos múltiplos puesto que siempre podrá ser multiplicado por un número cualquiera.
