El polígon regular

L'àrea del polígon regular és $A = \frac{P e r í m e t r e \cdot A p o t e m a}{2}$

El perímetre és: $P = n \cdot l$

on $l$ és la longitud del radi i $n$ el nombre de costats.

Exemple

Calcular l'àrea d'un hexàgon de $l = 10 c m$

Utilitzant Pitàgores es troba l'apotema $a$ , o alçada d'un dels sis triangles equilàters que formen l'hexàgon.

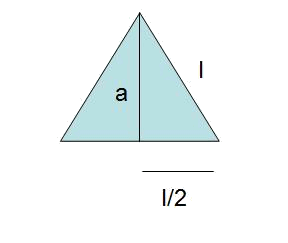
imagen

$l^{2} = a^{a} + (\frac{l}{2})^{2} a^{2} = l^{2} \cdot (1 - \frac{1}{4}) a = \frac{\sqrt{3}}{2} \cdot l$

Es troba l'àrea d'un dels triangles: $A_{t r i a n g l e} = \frac{l \cdot a}{2} = l^{2} \cdot \frac{\sqrt{3}}{4} = 25 \sqrt{3} c m^{2}$
Finalment es multiplica per $6$ per obtenir l'àrea total: $A_{h e x à g o n} = 150 \sqrt{3} c m^{2}$

Nota: Per a trobar àrees de polígons irregulars més complexos la filosofia serà la mateixa: trencar en triangles i sumar les àrees dels triangles.