El área del polígono regular es $$$A=\frac{Perímetro \cdot \ apotema}{2}$$$
El perímetro es: $$$P=n \cdot l$$$
dónde $$l$$ es la longitud del radio y $$n$$ el número de lados.
Calcular el área de un hexágono de $$l=10 \ cm$$
- Utilizando Pitágoras se encuentra el apotema $$a$$, o altura de uno de los seis triángulos equiláteros que forman el hexágono.
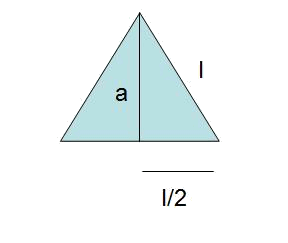
$$$l^2= a^a+ \Big(\frac{l}{2}\Big)^2 \\ a^2= l^2 \cdot \Big(1-\frac{1}{4}\Big) \\ a= \frac{\sqrt{3}}{2} \cdot l$$$
-
Se encuentra el área de uno de los triángulos: $$$A_{triángulo}=\frac{l·a}{2} = l^2 \cdot \frac{\sqrt{3}}{4}= 25 \sqrt{3} \ cm^2$$$
- Finalmente se multiplica por $$6$$ para obtener el área total: $$$A_{hexágono}=150\sqrt{3} \ cm^2$$$
Nota: Para encontrar áreas de polígonos irregulares más complejos la filosofía será la misma: romperlos en triángulos y sumar las áreas de los triángulos.
