Histograma

L'histograma és un representació semblant a un diagrama de barres, però se sol utilitzar quan el volum de dades és més ampli, o quan les variables són contínues.

Exemple

Les altures, en metres, d'un equip de bàsquet són les següents: $1.74, 1.84, 1.87, 1.92, 1.92, 1.97, 2.02, 2.03, 2.07, 2.11, 2.22$ Es poden realitzar diversos histogrames diferents. Si es defineixen intervals d'alçades o classes iguals (per exemple, de $10$ cm)

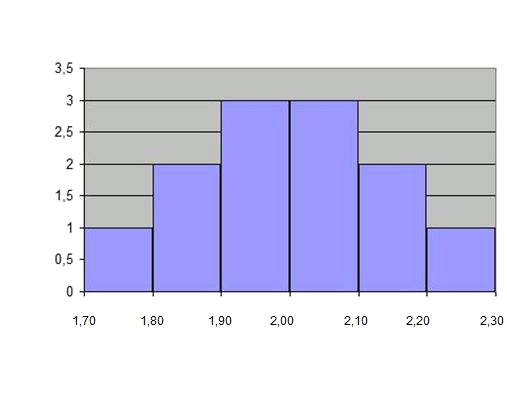
Els punts mitjans de cada interval són les marques de classes.

El diagrama serà equivalent a un diagrama de barres de les dades següents:

Interval d'altures (o classes)	Marques de classes	Freqüència absoluta
$[1.70, 1.80]$	$1.75$	$1$
$(1.80, 1.90]$	$1.85$	$2$
$(1.90, 2.00]$	$1.95$	$3$
$(2.00, 2.10]$	$2.05$	$3$
$(2.10, 2.20]$	$2.15$	$2$
$(2.20, 2.30]$	$2.25$	$1$

I l'histograma queda com un diagrama de barres, ja que els intervals són de mida constant:

imagen

No obstant això, es poden realitzar histogrames amb intervals diferents. Suposem que es volen veure barres que indiquin la quantitat de jugadors en cada posició.

Si els dos jugadors més baixos són bases, els tres següents escortes, els següents quatre alers i els tres més alts pivots. Quins intervals es poden definir?

Posició	Interval de altura
base	$[1.70, 1.85]$
escorta	$(1.85, 1.95]$
aler	$(1.95, 2.09]$
pívot	$(2.09, 2.25]$

Vegeu que són diversos els intervals que es poden definir.

La representació d'aquest nou histograma és:

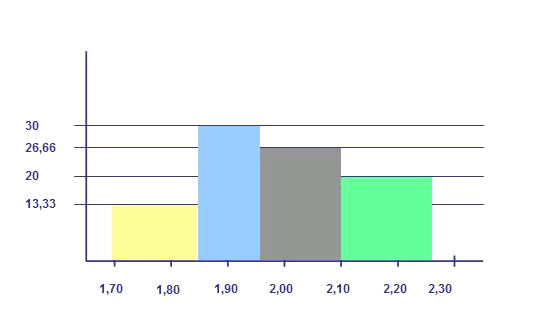
imagen

Es defineixen les alçades dels rectangles de manera que l'àrea de cada un tingui el valor de la freqüència absoluta de l'interval: $h_{i} = \frac{f_{i}}{a_{i}}$ amb $h$ l'alçada del rectangle que correspon a l'interval, $a_{i}$ a la seva amplitud, i $f$ la seva freqüència.

Nota: Totes les representacions explicades en aquest nivell es poden realitzar amb freqüències diferents de l'absoluta. Per exemple, es podrien dur a terme amb freqüències relatives (els histogrames tindrien la mateixa forma però altures normalitzades), o amb freqüències acumulades, de manera que l'histograma tindria una forma creixent de $0$ a $1$ semblant a la d'una funció distribució de probabilitat .