El histograma es un representación parecida a un diagrama de barras, pero se suele utilizar cuando el volumen de datos es más amplio, o cuando las variables son continuas.
Las alturas, en metros, de un equipo de baloncesto son las siguientes: $$$1.74, 1.84, 1.87, 1.92, 1.92, 1.97, 2.02, 2.03, 2.07, 2.11, 2.22$$$ Se pueden realizar varios histogramas distintos. Si se definen intervalos de alturas o clases iguales (por ejemplo, de $$10$$ cm)
Los puntos medios de cada intervalo son las marcas de clases.
El diagrama será equivalente a un diagrama de barras de los siguientes datos:
| Intervalo de alturas (o clases) | Marcas de clases | Frecuencia absoluta |
| $$[1.70, 1.80]$$ | $$1.75$$ | $$1$$ |
| $$( 1.80,1.90]$$ | $$1.85$$ | $$2$$ |
| $$( 1.90, 2.00]$$ | $$1.95$$ | $$3$$ |
| $$( 2.00, 2.10]$$ | $$2.05$$ | $$3$$ |
| $$( 2.10, 2.20]$$ | $$2.15$$ | $$2$$ |
| $$( 2.20, 2.30]$$ | $$2.25$$ | $$1$$ |
Y el histograma queda como un diagrama de barras, ya que los intervalos son de tamaño constante:
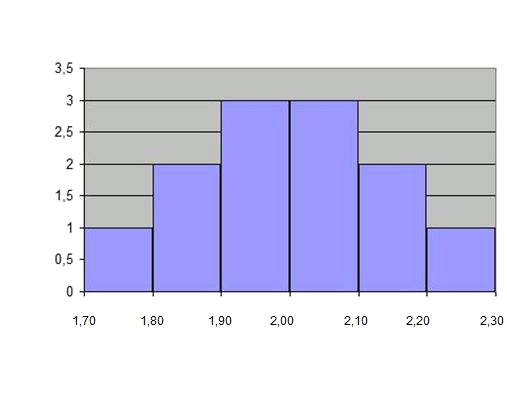
No obstante, se pueden realizar histogramas con intervalos distintos. Supóngase que se quieren ver barras que indiquen la cantidad de jugadores en cada posición.
Si los dos jugadores más bajos son bases, los tres siguientes escoltas, los siguientes cuatro aleros y los tres más altos pívots. ¿Qué intervalos se pueden definir?
| Posición | Intervalo de altura |
| base | $$[1.70, 1.85]$$ |
| escolta | $$( 1.85, 1.95]$$ |
| alero | $$( 1.95, 2.09]$$ |
| pívot | $$( 2.09, 2.25]$$ |
Véase que son varios los intervalos que se pueden definir.
La representación de este nuevo histograma es:
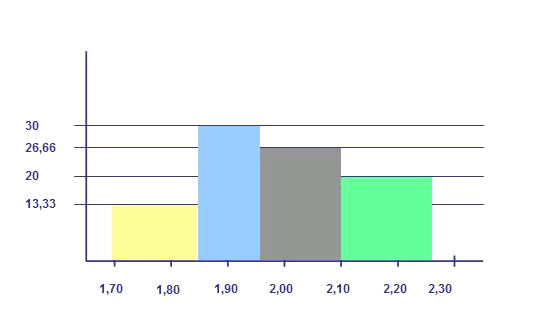
Se definen las alturas de los rectángulos de forma que el área de cada uno tenga el valor de la frecuencia absoluta del intervalo: $$h_i=\displaystyle \frac{f_i}{a_i}$$ con $$h$$ altura del rectángulo que corresponde al intervalo, $$a_i$$ a su amplitud, y $$f$$ su frecuencia.
Nota: Todas las representaciones explicadas en este nivel se pueden realizar con frecuencias distintas a la absoluta. Por ejemplo, se podrían llevar a cabo con frecuencias relativas (los histogramas tendrían la misma forma pero alturas normalizadas), o con frecuencias acumuladas, de forma que el histograma tendría una forma creciente de $$0$$ a $$1$$ parecida a la de una función distribución de probabilidad.