Parametrització de corbes

Sigui $C$ una corba en l'espai o en el pla. Una parametrització de $C$ és una funció $γ : [a, b] ⟶ R^{n}$ per a $n = 2$ o $3$ (en el pla o en l'espai), de manera que per a tot $t$ de l'interval $[a, b]$ , li assigna un punt del pla (i només un) o de l'espai. Aquesta $γ$ ha de ser una funció contínua i derivable.

Exemple

Una parametrització d'un cercle de radi $1$ és: $\begin{array}{ccc} γ : [0, 2 π] & ⟶ & R^{n} \\ θ & ⟶ & (\cos θ, \sin θ) \end{array}$ doncs per a cada punt $(x, y)$ del cercle, existeix algun $θ$ , tal que $γ (θ) = (x, y)$ .

Exemple

Una parametrització d'una el·lipse de semieixos $a$ i $b$ , $\begin{array}{ccc} γ : [0, 2 π] & ⟶ & R^{2} \\ θ & ⟶ & (a \cdot \cos θ, b \cdot \sin θ) \end{array}$

Exemple

Una parametrització d'una paràbola: $\begin{array}{ccc} γ : [0, 5] & ⟶ & R^{2} \\ t & ⟶ & (t, t^{2}) \end{array}$ En general si tenim una funció $f (x)$ podem parametritzar la seva gràfica com $γ (x) = (x, f (x))$ .

Exemple

Una parametrització del segment que uneix el punt del pla $(2, 3)$ amb $(- 1, 1)$ és $\begin{array}{ccc} γ : [0, 1] & ⟶ & R \\ t & ⟶ & t \cdot (\begin{matrix} 2 \\ 3 \end{matrix}) + (1 - t) \cdot (\begin{matrix} - 1 \\ 1 \end{matrix}) \end{array}$

Exemple

La parametrització $\begin{array}{ccc} γ : [0, 5] & ⟶ & R^{3} \\ t & ⟶ & (\cos t, \sin t, t) \end{array}$ és d'una espiral. Per veure-ho amb més claredat, és recomanable mirar com seria la gràfica si eliminem una component, és a dir, si traiem la tercera component (si veiés la figura des de dalt), tenim un cercle, l'alçada va augmentant, així que tenim una espiral.

Exemple

La parametrització del segment que uneix els punts de l'espai $(0, 0, 1)$ i $(3, 2, 0)$ és $\begin{array}{ccc} γ : [0, 1] & ⟶ & R \\ t & ⟶ & t \cdot (\begin{matrix} 0 \\ 0 \\ 1 \end{matrix}) + (1 - t) \cdot (\begin{matrix} 3 \\ 2 \\ 0 \end{matrix}) \end{array}$

Exemple

Una parametrització d'un cercle de radi $1$ , posat pla però a una alçada de $z = 3$ , ve donada per la funció $\begin{array}{ccc} γ : [0, 2 π] & ⟶ & R^{3} \\ θ & ⟶ & (\cos θ, \sin θ, 3) \end{array}$

Donada una corba $C$ del pla o de l'espai, per obtenir la seva parametrització $γ$ es pot procedir de diverses formes. De vegades, farem servir una de les coordenades com a variable de la parametrització, com en l'exemple 3: Si tenim una gràfica d'una funció, aquesta mateixa ja ens servirà com a parametrització. És a dir:

Sigui $f (x)$ una funció contínua i derivable, aleshores $γ (x) = (x, f (x))$ és una parametrització de la seva gràfica.

Però això no serveix, per exemple, amb un cercle (exemple 1), ja que el cercle té, per a cada $x$ , dos valors diferents de $y$ . Com a molt podem parametritzar la meitat superior del cercle.

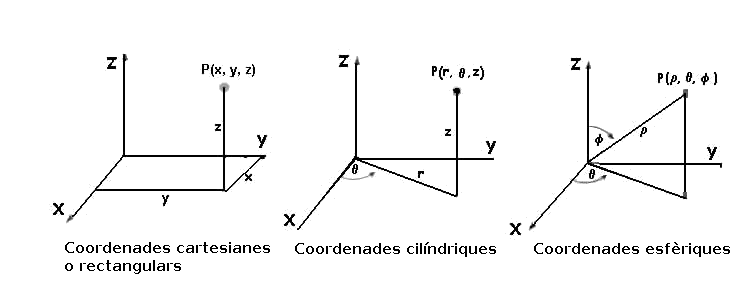
Una altra forma d'obtenir parametritzacions de corbes, és prenent diferents sistemes de coordenades, com per exemple les coordenades esfèriques (radi i 2 angles), o cilíndriques (radi, alçada i angle).

imagen