Sea $$C$$ una curva en el espacio o en el plano. Una parametrización de $$C$$ es una función $$$\gamma:[a,b] \longrightarrow \mathbb{R}^{n}$$$ por $$n=2$$ o $$3$$ (en el plano o en el espacio), de forma que para todo $$t$$ del intervalo $$[a, b]$$, le asigna un punto del plano (y sólo un punto) o del espacio. Esta $$\gamma$$ debe ser una función continua y derivable.
Una parametrización de un círculo de radio $$1$$: $$$\begin{array} {ccc} \gamma: [0,2 \pi] & \longrightarrow & \mathbb {R} ^{n} \\ \theta & \longrightarrow & (\cos \theta, \sin \theta) \end{array}$$$ pues para cada punto $$(x,y)$$ del círculo, existe algún $$\theta$$ , tal que $$\gamma(\theta)=(x,y)$$.
Una parametrización de una elipse de semiejes $$a$$ y $$b$$, $$$ \begin{array} {ccc} \gamma: [0,2 \pi] & \longrightarrow & \mathbb {R} ^{2} \\ \theta & \longrightarrow & (a \cdot \cos \theta, b \cdot \sin \theta) \end{array}$$$
Una parametrización de una parábola: $$$\begin{array} {ccc} \gamma: [0,5] & \longrightarrow & \mathbb {R} ^{2} \\ t & \longrightarrow & (t, t^{2}) \end{array}$$$ En general, si tenemos una función $$f(x)$$ podemos parametrizar su gráfica como $$\gamma (x) = (x,f(x))$$.
Una parametrización del segmento que une el punto del plano $$(2,3)$$ con el $$(-1,1)$$ es $$$\begin{array} {ccc} \gamma: [0,1] & \longrightarrow & \mathbb {R} \\ t & \longrightarrow & t \cdot \left(\begin{array}{c} 2 \\ 3 \end{array}\right) + (1-t) \cdot \left( \begin{array}{c} -1 \\ 1\end{array}\right) \end{array}$$$
La parametrización $$$\begin{array} {ccc} \gamma: [0,5] & \longrightarrow & \mathbb {R} ^{3} \\ t & \longrightarrow & (\cos t, \sin t, t) \end{array}$$$ es de una espiral. Para verlo con más claridad, es recomendable mirar cómo seria la gráfica si eliminamos una componente. Si, por ejemplo, quitamos la tercera componente (si vieramos la figua desde arriba), tenemos un círculo y la altura va aumentando, así que tenemos una espiral.
La parametrización del segmento que une los puntos del espacio $$(0,0,1)$$ y $$(3,2,0)$$ es $$$\begin{array} {ccc} \gamma: [0,1] & \longrightarrow & \mathbb {R} \\ t & \longrightarrow & t \cdot \left(\begin{array}{c} 0 \\ 0 \\ 1 \end{array}\right)+(1-t) \cdot \left(\begin{array}{c} 3 \\ 2 \\ 0 \end{array}\right) \end{array}$$$
Una parametrización de un círculo de radio $$1$$, puesto plano pero a una altura de $$z=3$$, viene dada por la función $$$ \begin{array} {ccc} \gamma: [0,2 \pi] & \longrightarrow & \mathbb {R} ^{3} \\ \theta & \longrightarrow & (\cos \theta, \sin \theta, 3) \end{array}$$$
Dada una curva $$C$$ del plano o del espacio, para obtener su parametrización $$\gamma$$ se puede proceder de varias formas. Algunas veces, usaremos una de las coordenadas como variable de la parametrización, como en el ejemplo 3. Si tenemos una gráfica de una función, ésta misma ya nos servirá como parametrización. Es decir:
- Sea $$f(x)$$ una función continua y derivable, entonces $$\gamma(x)=(x,f(x))$$ es una parametrización de su gráfica.
Pero esto no sirve, por ejemplo, con un círculo (ejemplo 1), pues el círculo tiene, para cada $$x$$, dos valores distintos de $$y$$. Como mucho podemos parametrizar la mitad superior del círculo.
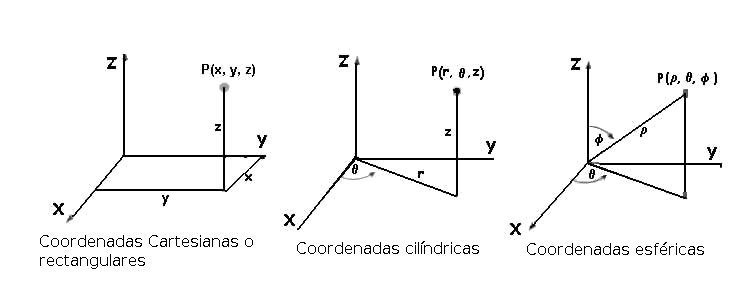
- Otra forma de obtener parametrizaciones de curvas, es tomando distintos sistemas de coordenadas, como por ejemplo las coordenadas esféricas (radio y 2 ángulos), o cilíndricas (radio, altura y ángulo).