Un sistema d'equacions és no lineal si, si més no, una de les seves equacions no és lineal (hi ha un grau més gran que 1).
Aquests sistemes es resoldran habitualment per substitució. És recomanable dibuixar les equacions del sistema en la mesura del possible per fer-se una idea aproximada de la situació de les solucions, si n'hi ha.
Trobar les solucions, si n'hi ha, de $$$\left\{ \begin{array}{c} x^2+y^2=25 \\ x+y=5 \end{array} \right.$$$
Com s'ha comentat, resulta interessant dibuixar a grans trets les funcions. Encara sense dibuixar, es detecta que la primera equació és la d'una circumferència centrada en $$(0,0)$$ i de radi $$5$$. Per això, poden passar tres situacions:
- Que no hi hagi cap solució: La recta passa sense tallar la circumferència (per sobre o per sota).
- Que només hi hagi una solució: La recta és tangent a la circumferència (per sobre o per sota).
- Que hi hagi dues solucions: La recta talla dues vegades la circumferència.
En l'exemple proposat s'observa fàcilment que hi haurà dues solucions:
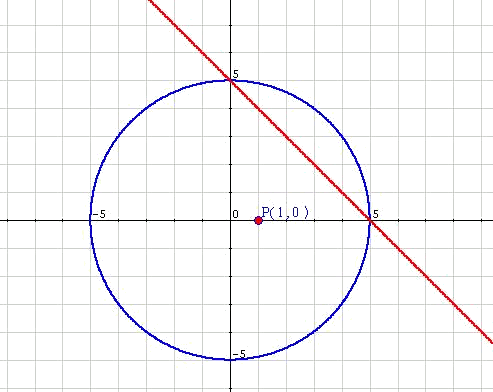
Resolució analítica:
1) S'aïlla una variable en una de les equacions (serà més fàcil començar per la de primer grau) $$$y=5-x$$$
2) Es substitueix la variable aïllada en l'altra equació $$$x^2+(5-x)^2=25$$$
3) Es resol: $$$x^2+25-10x+x^2=25 \\ 2x^2-10x=0 \\ x\cdot(2x-10)=0 \\ x_1=0 \\ 2x-10=0 \rightarrow x_2=5$$$
4) I, substituint en l'altra equació, $$$x_1=0 \Rightarrow y_1=5$$$ $$$x_2=5 \Rightarrow y_2=0$$$
Es pot veure que el resultat analític concorda amb l'aproximació gràfica.
Cal insistir en la necessitat d'intentar imaginar (si no es disposa de calculadores o ordinadors) la representació gràfica abans de resoldre. Això permetrà una resolució enfocada a un resultat, la qual cosa és sempre més efectiu que resoldre el sistema sense cap idea aproximada de què s'obtindrà.