Un sistema de ecuaciones es no lineal si, por lo menos, una de sus ecuaciones no es lineal (hay un grado mayor que uno).
Estos sistemas se resolverán habitualmente por sustitución. Es recomendable dibujar las ecuaciones del sistema en la medida de lo posible para hacerse una idea aproximada de la situación de las soluciones, si las hay.
Encontrar las soluciones, si las hay, de $$$\left\{ \begin{array}{c} x^2+y^2=25 \\ x+y=5 \end{array} \right.$$$
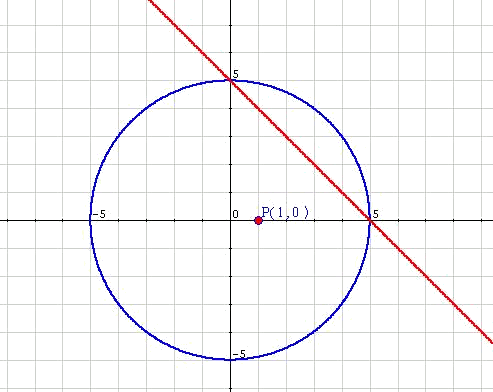
Como se ha comentado, resulta interesante dibujar a grandes rasgos las funciones. Aún sin dibujarlas, se detecta que la primera ecuación es la de una circunferencia centrada en $$(0,0)$$ y de radio $$5$$. Por ello, pueden ocurrir tres situaciones:
- Que no exista ninguna solución: La recta pasa sin cortar la circunferencia (por encima o por debajo).
- Que sólo exista una solución: La recta es tangente a la circunferencia (por encima o por debajo).
- Que existan dos soluciones: La recta corta dos veces la circunferencia.
En el ejemplo propuesto se observa fácilmente que habrá dos soluciones:
Resolución analítica:
1) Se despeja una variable en una de las ecuaciones (será más fácil empezar por la de primer grado) $$$y=5-x$$$
2) Se sustituye la variable despejada en la otra ecuación $$$x^2+(5-x)^2=25$$$
3) Se resuelve: $$$x^2+25-10x+x^2=25 \\ 2x^2-10x=0 \\ x\cdot(2x-10)=0 \\ x_1=0 \\ 2x-10=0 \rightarrow x_2=5$$$
4) Y, sustituyendo en la otra ecuación, $$$x_1=0 \Rightarrow y_1=5$$$ $$$x_2=5 \Rightarrow y_2=0$$$
Se puede ver que el resultado analítico concuerda con la aproximación gráfica.
Hay que insistir en la necesidad de intentar imaginar (si no se dispone de calculadoras o ordenadores) la representación gráfica antes de resolver. Esto permitirá una resolución enfocada a un resultado, lo cual es siempre más efectivo que resolver el sistema sin ninguna idea aproximada de qué se obtendrá.