Let's see now the definitions of relative and absolute extrema by means of an example:
-
A function f has a relative or local minimum (respectively relative or local maximum) in
- A function
Example
Consider the following function:
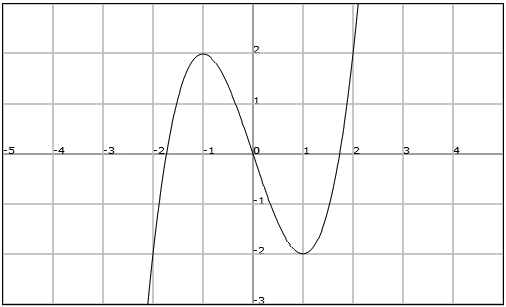
We observe that it has:
- Relative maximum in
- The function is odd and it is not bounded.
