Vegem ara les definicions d'extrems relatius i absoluts acompanyades d'un exemple:
-
Una funció $$f$$ té un mínim relatiu o local (respectivament màxim relatiu o local) en $$x = a$$, si existeix un entorn del punt $$a$$, $$E_r(a)$$ tal que per a tot $$x$$ pertanyent a aquest entorn, es té que $$$f(x)\leq f(a) (\mbox{ respectivament } f(x)\geq f(a))$$$
- Una funció $$f$$ té un mínim absolut (respectivament màxim absolut) en $$x = a$$, si per qualsevol $$x$$ del domini de $$f$$ es verifica que $$$f(x)\leq f(a) (\mbox{ respectivament }f(x)\geq f(a))$$$
Donada la següent funció:
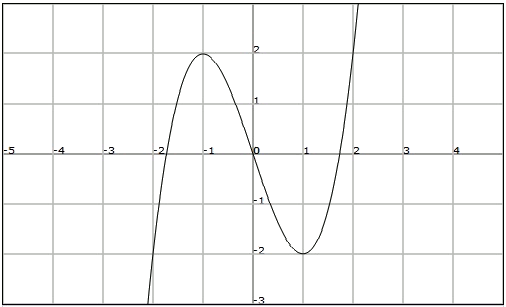
Observem que presenta:
- Màxim relatiu en $$x = -1$$, mínim relatiu en $$x = 1$$.
- La funció és senar i no està fitada.
