Observa la funció de l'exemple anterior. El valor màxim que prenen les imatges és $$1$$. Direm que la funció està fitada superiorment per $$1$$.
Una funció $$f$$ està fitada superiorment si existeix un nombre real $$K$$ tal que per a tot $$x$$ pertanyent al domini de $$f$$, $$f (x) \leq K$$. Direm que $$K$$ és una fita superior de la funció.
Ens podem fixar ara que el mínim valor que prenen les imatges és $$0$$. Direm que la funció està fitada inferiorment.
Una funció $$f$$ està fitada inferiorment si existeix un nombre real $$K'$$ tal que per a tot $$x$$ pertanyent al domini de $$f$$, $$f (x) \geq K'$$. Direm que $$K'$$ és una fita inferior de la funció.
És destacable el fet que si $$K$$ és una fita superior d'una funció, qualsevol altre número més gran que $$K$$ també ho és. Així mateix, si $$K'$$ és una fita inferior de la funció, qualsevol altre nombre menor que $$K'$$ també ho és.
Indica si la funció del dibuix està fitada, i troba cotes superiors i inferiors quan procedeixi.
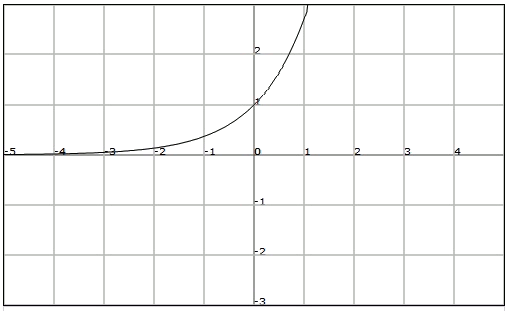
Observem que la funció està fitada inferiorment, però en canvi no ho està superiorment.
Per tant direm que globalment no està acotada i una fita inferior és $$K = 0$$.