Observa la función del ejemplo anterior. El valor máximo que toman las imágenes es $$1$$. Diremos que la función está acotada superiormente por $$1$$.
Una función $$f$$ está acotada superiormente si existe un número real $$K$$ tal que, para todo $$x$$ perteneciente al dominio de $$f$$, $$f (x) \leq K$$. Diremos que $$K$$ es una cota superior de la función.
Nos podemos fijar ahora en que el mínimo valor que toman las imágenes es $$0$$. Diremos que la función está acotada inferiormente.
Una función $$f$$ está acotada inferiormente si existe un número real $$K'$$ tal que, para todo $$x$$ perteneciente al dominio de $$f$$, $$f (x) \geq K'$$. Diremos que $$K'$$ es una cota inferior de la función.
Es destacable el hecho que si $$K$$ es una cota superior de una función, cualquier otro número mayor que $$K$$ también lo es. Asimismo, si $$K'$$ es una cota inferior de la función, cualquier otro número menor que $$K'$$ también lo es.
Indica si la función del dibujo está acotada, y encuentra cotas superiores e inferiores cuando proceda.
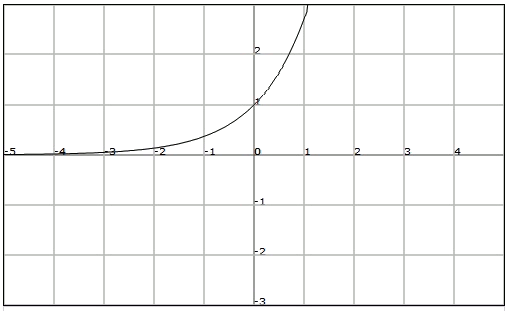
Observamos que la función está acotada inferiormente, pero en cambio no lo está superiormente.
Por tanto diremos que globalmente no está acotada y una cota inferior es $$K = 0$$.
