Consideremos la gráfica de la siguiente función $$f(x)=x^2$$:
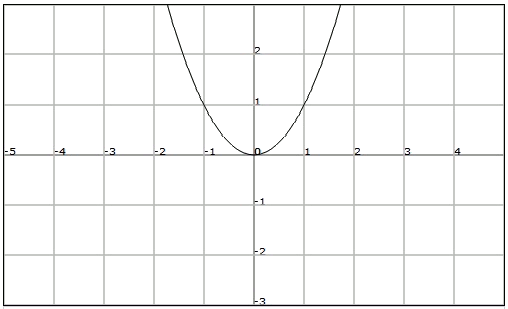
Observamos que cualquier número $$x$$ y su opuesto $$-x$$ tienen la misma imagen. En este caso decimos que la función es par.
Una función $$f$$ es par si para cualquier $$x$$ del dominio se verifica: $$$f(x)=f(-x)$$$
Observemos que las funciones pares son simétricas respecto del eje vertical.
Consideremos ahora la función $$f(x)=x^3$$:
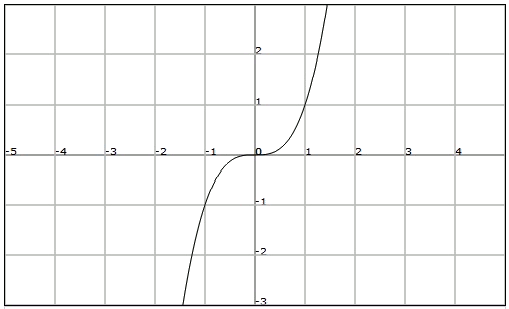
Observamos que cualquier número $$x$$ y su opuesto $$-x$$ tienen imágenes opuestas. En este caso decimos que la función f es impar.
Una función $$f$$ es impar si para cualquier $$x$$ del dominio se verifica: $$$f(x)=-f(-x)$$$
Dadas la siguientes funciones, decidid cuáles de ellas son pares o impares: $$$\displaystyle f(x)=\frac{1}{x} \mbox{ y } g(x)=x^2-2$$$
Comprobamos si las funciones son pares: $$$f(x)=f(-1) \Longleftrightarrow \displaystyle \frac{1}{x}=\frac{1}{-x} \Longleftrightarrow 1= -1 !! \\ g(x)=g(-x) \Longleftrightarrow x^2-2=(-x)^2-2=x^2-2 \mbox{ OK }$$$
Comprobamos si la función $$f$$ es impar ($$g$$ no lo será ya que es par): $$$\displaystyle f(x)=-f(-x) \Longleftrightarrow \frac{1}{x}=-\frac{1}{-x}=\frac{1}{x} \mbox{ OK }$$$
Por tanto la función $$f$$ es impar, y la función $$g$$ es par.
