Even and odd functions

Let's consider the graph of the following function f(x)=x2:

imagen

We observe that any number x and its opposite −x have the same image. In this case we say that the function is a pair.

A function f is a pair if for any x in the domain we have: f(x)=f(−x)

Note that even functions are symmetrical with regard to the vertical axis.

Let's consider now the function f(x)=x3:

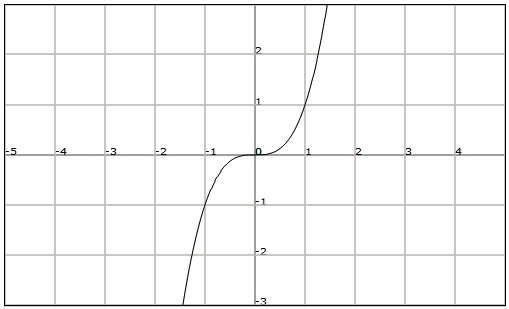
imagen

We know that any number x and its inverse −x have inverse images. In this case we say that the function f is odd.

A function f is odd if for any x in the domain we have:f(x)=−f(−x)

Example

Given following functions, decide which of them are even or odd: f(x)=1x and g(x)=x2−2

Let's verify if the functions are even: f(x)=f(−1)⟺1x=1−x⟺1=−1!!g(x)=g(−x)⟺x2−2=(−x)2−2=x2−2 OK 

Let's verify if the function f is odd (g will not be odd since it is an even function): f(x)=−f(−x)⟺1x=−1−x=1x OK 

Therefore the function f is odd, and the function g is a pair.