Observe the following function:
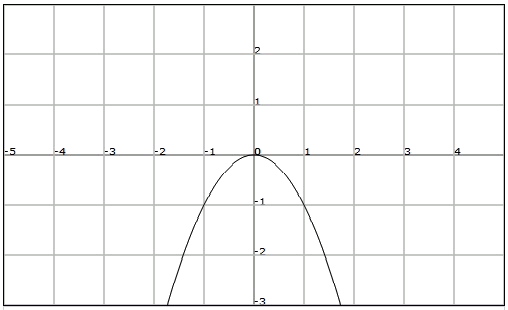
We observe in the interval $$(-\infty, 0)$$, when $$x$$ increases the value of $$f(x)$$ also increases. We say then that the function is increasing in the interval $$(-\infty, 0)$$.
A function $$f$$ is strictly increasing in an interval of its domain if it is verified of $$x_1$$ and $$x_2$$ ,belonging to the above mentioned interval, that: $$$x_1 < x_2 \Rightarrow f(x_1) < f(x_2)$$$
On the other hand, in the interval $$(0, +\infty)$$, in the previous graph, we see that as the value of $$x$$ increases that of $$f(x)$$ decreases. In this case we say that the function is decreasing.
A function $$f$$ is strictly decreasing in an interval of its domain if $$x_1$$ and $$x_2$$, which to the above mentioned interval, give:$$$x_1 < x_2 \Rightarrow f(x_1) > f(x_2)$$$
If a function is only increasing or decreasing in an interval of its domain we say that the function is monotonic in that interval.
Although we have defined increasing and decreasing functions in an interval, we can also define increasing or decreasing functions:
A function $$f$$ is increasing in an interval of its domain if $$x_1$$ and $$x_2$$, each belonging to the above mentioned interval, satisfy: $$$x_1 < x_2 \Rightarrow f(x_1)\leq f(x_2)$$$
A function $$f$$ is decreasing in an interval of its domain if $$x_1$$ and $$x_2$$, each belonging to the above mentioned interval, satisfy: $$$x_1 < x_2 \Rightarrow f(x_1) \geq f(x_2)$$$
Note that the difference between these definitions is that the latter allows the possibility that $$f(x_1)=f(x_2)$$.