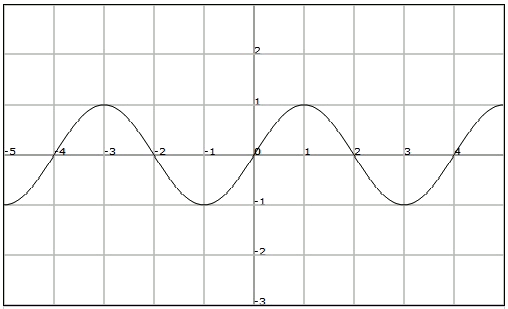
Concentrate on the function represented in the previous figure. The images of $$$ \ldots,-4,-2, 0, 2, 4,\ldots$$$ coincide and they are equal to $$0$$.
In fact we can observe that the image of any real number $$x$$ with the images of $$$x + 2, x + 4,\ldots$$$ We will say that the function is periodic.
A function $$f$$ is periodic of period $$T$$ if it exists a positive real number $$T$$ such that for any $$x$$ of the domain we have that:$$$f (x + T) = f (x)$$$Note that if $$T$$ is a period of the function then also any multiple of $$T$$ is also a period. The minimum value of $$T$$ that satisfies the previous definition is known as the fundamental period.
Find the fundamental period of the following function:
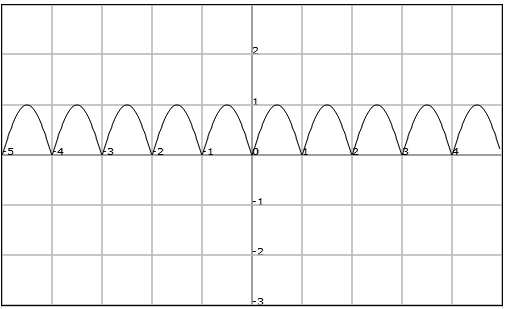
We observe that the function takes the value $$0$$ in each integer, and has the same behaviour between any $$n$$ and $$n + 1$$.
Therefore, since there are no other regularity for shorter periods, we will have that the fundamental period of $$f$$ is $$T = 1$$.