In the graph of a function we can observe certain characteristics of the functions that give us information about its behaviour.
Observe the graphs of the functions $$f(x)=x^2$$ and $$g(x)=2x$$
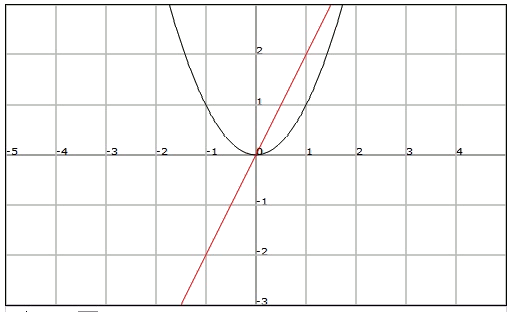
For the function $$f$$, we observe that we can trace at least one horizontal straight line ($$y$$ = constant) that the cuts the graph in more than one point.
For example, if we consider the horizontal straight line $$y = 4$$, we see that there are two points in the domain of $$f$$, $$x = 2$$, and $$x = -2$$, with have the same image $$f (x) = 4$$.
On the other hand, any horizontal straight line traced on the graph of the function $$g$$ will cut its graph only once. Therefore, there aren't any two elements in the domain of $$g$$ that have the same image.
A function $$f$$ is injective if every two different elements in its domain have two different images, that is, if it is satisfied that: $$$x_1\neq x_2 \Longrightarrow f(x_1)\neq f(x_2)$$$
Therefore we observe that the function $$g$$ is injective while $$f$$ is not.
If we consider again the functions $$f$$ and $$g$$, we observe that: The graph of the function $$f$$ lies on the positive side of the $$y$$-axis, thus $$Im(f)=[0,+\infty)$$.
On the other hand, the graph of the function $$g$$ is on all the real numbers, thus $$Im(g)=\mathbb{R}$$.
A function $$f$$ is exhaustive if its graph coincides with the set of the real numbers, that is, if we have that:$$$Im (f)=\mathbb{R}$$$
We have therefore that the function $$f$$ is not exhaustive and that the function $$g$$ is exhaustive.
Finally
A function is bijective if it is injective and exhaustive simultaneously.
This way the function $$g$$ of the example is bijective while the function $$f$$ is not.
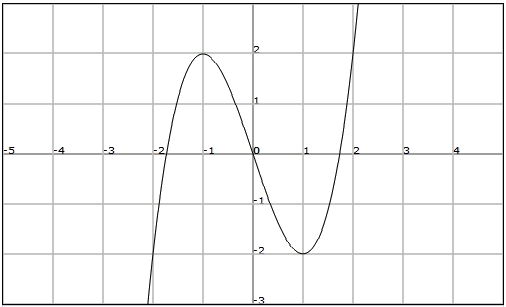
Determine if the function $$f$$ represented in the following figure is injective, exhaustive or bijective:
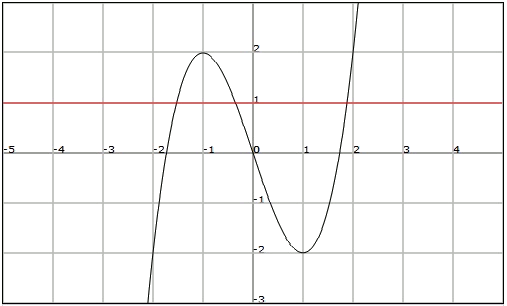
First, we should realize that the function is not injective since we can trace the straight line $$y = 1$$, cutting the graph in more than one point. This means that different values of the independent variable $$x$$ have the same image.
On the other hand, the function $$f$$ is exhaustive since all the real numbers are in its image, that is $$Im (f)=\mathbb{R}$$.
Obviously the function will not be bijective since it is not injective.