En la gráfica de una función podemos observar determinadas características de las funciones que nos aportan información sobre su comportamiento.
Observad las gráficas de las funciones y
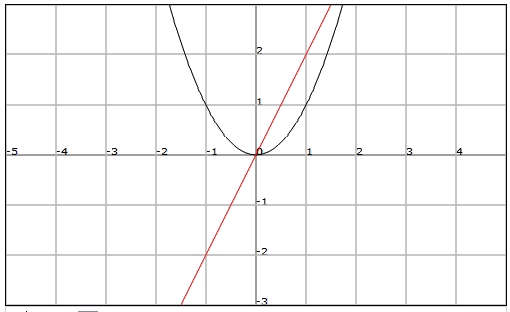
Para la función , observamos que podemos trazar al menos una recta horizontal ( = constante ) que la corte en más de un punto.
Por ejemplo, si consideramos la recta horizontal , vemos que hay dos elementos diferentes del dominio de , , y , que tienen la misma imagen .
En cambio, cualquier recta horizontal trazada sobre la gráfica de la función corta como máximo un punto de dicha función. Por tanto, no hay dos elementos distintos del dominio que tengan la misma imagen.
Una función es inyectiva si dos elementos distintos cualesquiera de su dominio tienen imágenes distintas por , es decir, si se cumple:
Por tanto observamos que la función es inyectiva mientras que no lo es.
Si consideramos otra vez las funciones y , observamos que:
El recorrido de la función son los números reales mayores o iguales que cero, es decir, .
En cambio, el recorrido de la función son todos los números reales, es decir, .
Una función es exhaustiva si su recorrido coincide con el conjunto de los números reales, es decir, si se cumple:
Tenemos por tanto que la función no es exhaustiva y en cambio la función si que lo es.
Por último:
Una función es biyectiva si es inyectiva y exhaustiva a la vez.
Así la función del ejemplo es biyectiva mientras que la función no lo es.
Ejemplo
Determinad si la función representada en la siguiente figura es inyectiva, exhaustiva y biyectiva:
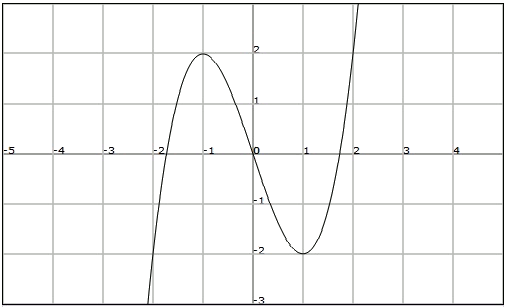
Fijémonos en que la función no es inyectiva ya que podemos trazar la recta , que corta la gráfica de en más de un punto. Esto significa que distintos valores de la variable independiente tienen la misma imagen.
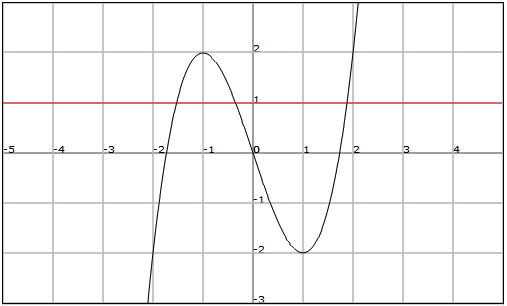
En cambio, la función si que es exhaustiva ya que su imagen son todos los números reales, es decir, .
Evidentemente la función no será biyectiva ya que no es inyectiva.



