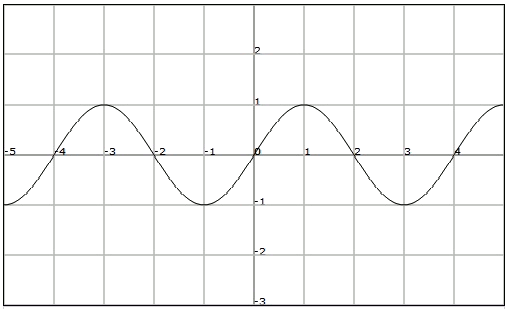
Fíjate en la función representada en la figura anterior. Las imágenes de $$$ \ldots,-4,-2, 0, 2, 4,\ldots$$$ coinciden y son iguales a $$0$$.
De hecho podemos observar que la imagen de cualquier número real $$x$$ que consideremos coincide con las imágenes de $$$x + 2, x + 4,\ldots$$$ Diremos que la función es periódica.
Una función $$f$$ es periódica de periodo $$T$$ si existe un número real positivo $$T$$ tal que para cualquier $$x$$ del dominio de la función se tiene $$$f (x + T) = f (x)$$$
Si $$T$$ es un periodo de la función, lógicamente también lo será un múltiplo cualquiera de $$T$$. El mínimo valor de $$T$$ que cumple la definición anterior se conoce como periodo fundamental.
Encuentra el periodo fundamental de la función siguiente:
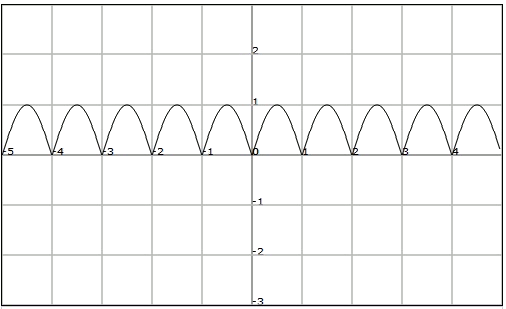
Observamos que la función vale $$0$$ para cada número natural, y repite su comportamiento entre $$n$$ y $$n + 1$$.
Por tanto, al no haber una periodicidad de periodo menor, tendremos que el periodo fundamental de $$f$$ es $$T = 1$$.
