Veamos ahora las definiciones de extremos relativos y absolutos acompañadas de un ejemplo:
-
Una función $$f$$ tiene un mínimo relativo o local (respectivamente máximo relativoo local) en $$x = a$$, si existe un entorno del punto $$a$$, $$E_r(a)$$ tal que para todo $$x$$ perteneciente a dicho entorno, se tiene que $$$f(x)\leq f(a) (\mbox{ respectivamente } f(x)\geq f(a))$$$
- Una función $$f$$ tiene un mínimo absoluto (respectivamente máximo absoluto) en $$x = a$$, si para cualquier $$x$$ del dominio de $$f$$ se verifica que $$$f(x)\leq f(a) (\mbox{ respectivamente }f(x)\geq f(a))$$$
Dada la siguiente función:
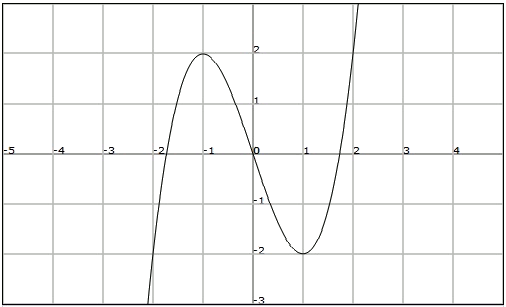
Observamos que presenta:
- Máximo relativo en $$x =-1$$, mínimo relativo en $$x = 1$$.
- La función es impar y no está acotada.
