Observa la siguiente función:
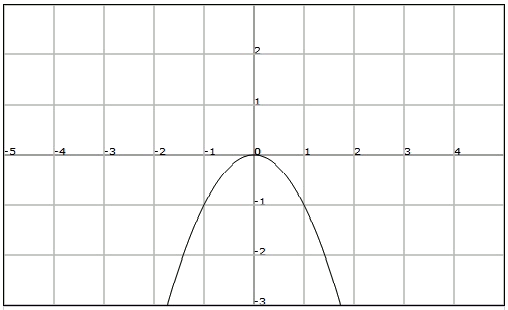
Observamos que en el intervalo $$(-\infty, 0)$$, al aumentar el valor de $$x$$ también aumenta el valor de $$f(x)$$. Decimos entonces que la función es estrictamente creciente en el intervalo $$(-\infty, 0)$$.
Una función $$f$$ es estrictamente creciente en un intervalo de su dominio si dados $$x_1$$ y $$x_2$$, pertenecientes a dicho intervalo, se verifica que: $$$x_1 < x_2 \Rightarrow f(x_1) < f(x_2)$$$
Por otro lado, en el intervalo $$(0, +\infty)$$, de la gráfica anterior, vemos que a medida que aumenta el valor de $$x$$ disminuye el de $$f(x)$$. En este caso decimos que la función es estrictamente decreciente.
Una función $$f$$ es estrictamente decreciente en un intervalo de su dominio si dados $$x_1$$ y $$x_2$$, pertenecientes a dicho intervalo, se verifica que: $$$x_1 < x_2 \Rightarrow f(x_1) > f(x_2)$$$
Si una función es únicamente creciente o decreciente en un intervalo de su dominio decimos que la función es monótona en dicho intervalo.
Aunque hemos definido funciones estrictamente crecientes o estrictamente decrecientes en un intervalo, también se puede definir funciones crecientes o decrecientes:
Una función $$f$$ es creciente en un intervalo de su dominio si dados $$x_1$$ y $$x_2$$, pertenecientes a dicho intervalo, se verifica que: $$$x_1 < x_2 \Rightarrow f(x_1)\leq f(x_2)$$$
Una función $$f$$ es decreciente en un intervalo de su dominio si dados $$x_1$$ y $$x_2$$, pertenecientes a dicho intervalo, se verifica que: $$$x_1 < x_2 \Rightarrow f(x_1) \geq f(x_2)$$$
Observamos pues que la diferencia está en admitir $$f(x_1)=f(x_2)$$.