Observa la següent funció:
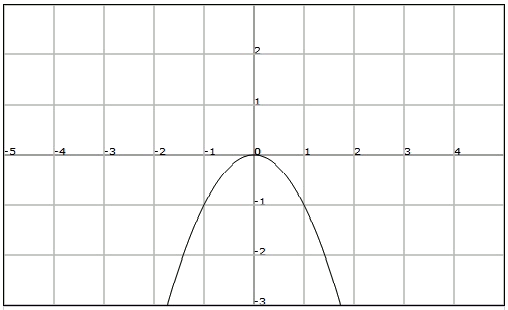
Observem que en l'interval $$(-\infty, 0)$$, en augmentar el valor de $$x$$ també augmenta el valor de $$f(x)$$. Diem llavors que la funció és estrictament creixent en l'interval $$(-\infty, 0)$$.
Una funció $$f$$ és estrictament creixent en un interval del seu domini si donats $$x_1$$ i $$x_2$$, pertanyents a l'interval, es verifica: $$$x_1 < x_2 \Rightarrow f(x_1) < f(x_2)$$$
D'altra banda, en l'interval $$(0, +\infty)$$, de la gràfica anterior, veiem que a mesura que augmenta el valor de $$x$$ disminueix el de $$f(x)$$. En aquest cas diem que la funció és estrictament decreixent.
Una funció $$f$$ és estrictament decreixent en un interval del seu domini si donats $$x_1$$ i $$x_2$$, pertanyents a aquest interval, es verifica que: $$$x_1 < x_2 \Rightarrow f(x_1) > f(x_2)$$$
Si una funció és únicament creixent o decreixent en un interval del seu domini diem que la funció és monòtona en aquest interval.
Tot i que hem definit funcions estrictament creixents o estrictament decreixents en un interval, també es pot definir funcions creixents o decreixents:
Una funció $$f$$ és creixent en un interval del seu domini si donats $$x_1$$ i $$x_2$$, pertanyents a aquest interval, es verifica que: $$$x_1 < x_2 \Rightarrow f(x_1)\leq f(x_2)$$$
Una funció $$f$$ és decreixent en un interval del seu domini si donats $$x_1$$ i $$x_2$$, pertanyents a aquest interval, es verifica que: $$$x_1 < x_2 \Rightarrow f(x_1) \geq f(x_2)$$$
Observem doncs que la diferència està en admetre $$f(x_1)=f(x_2)$$.