A la gràfica d'una funció podem observar determinades característiques de les funcions que ens aporten informació sobre el seu comportament.
Observeu les gràfiques de les funcions $$f(x)=x^2$$ i $$g(x)=2x$$
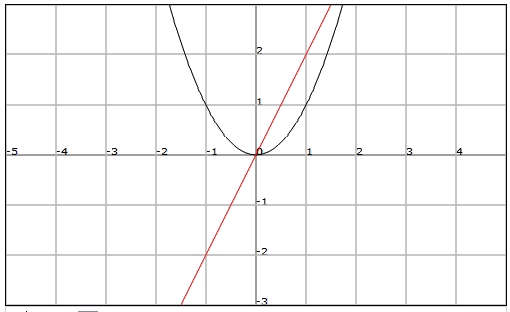
Per a la funció $$f$$, observem que podem traçar almenys una recta horitzontal ($$y$$ = constant) que la talla en més d'un punt.
Per exemple, si considerem la recta horitzontal $$y = 4$$, veiem que hi ha dos elements diferents del domini de $$f$$, $$x = 2$$, i $$x = -2$$, que tenen la mateixa imatge $$f (x) = 4$$.
En canvi, qualsevol recta horitzontal traçada sobre la gràfica de la funció g curta com a màxim un punt d'aquesta funció. Per tant, no hi ha dos elements diferents del domini que tinguin la mateixa imatge.
Una funció $$f$$ és injectiva si dos elements diferents qualssevol del seu domini tenen imatges diferents per $$f$$, és a dir, si es compleix: $$$x_1\neq x_2 \Longrightarrow f(x_1)\neq f(x_2)$$$
Per tant observem que la funció $$g$$ és injectiva mentre que $$f$$ no ho és.
Si considerem una altra vegada les funcions $$f$$ i $$g$$, observem que:
El recorregut de la funció $$f$$ són els nombres reals més grans o iguals que zero, és a dir, $$Im(f)=[0,+\infty)$$.
En canvi, el recorregut de la funció $$g$$ són tots els nombres reals, és a dir, $$Im(g)=\mathbb{R}$$.
Una funció $$f$$ és exhaustiva si el seu recorregut coincideix amb el conjunt dels nombres reals, és a dir, si es compleix: $$$Im (f)=\mathbb{R}$$$
Tenim per tant que la funció $$f$$ no és exhaustiva i en canvi la funció $$g$$ sí que ho és.
Finalment:
Una funció és bijectiva si és injectiva i exhaustiva alhora.
Així la funció $$g$$ de l'exemple és bijectiva mentre que la funció $$f$$ no ho és.
Determineu si la funció $$f$$ representada en la figura següent és injectiva, exhaustiva i bijectiva:
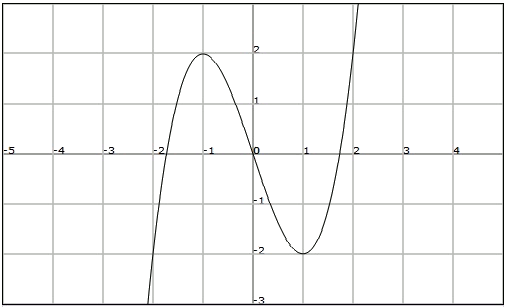
Fixem-nos que la funció no és injectiva ja que podem traçar la recta $$y = 1$$, que talla la gràfica de $$f$$ en més d'un punt. Això vol dir que diferents valors de la variable independent $$x$$ tenen la mateixa imatge.
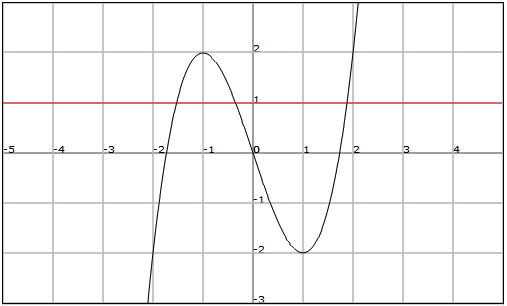
En canvi, la funció si que és exhaustiva ja que la seva imatge són tots els nombres reals, és a dir, $$Im (f)=\mathbb{R}$$.
Evidentment la funció no serà bijectiva ja que no és injectiva.