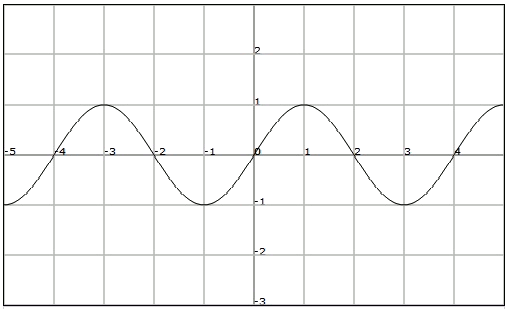
Fixa't en la funció representada en la figura anterior. Les imatges de $$$ \ldots,-4,-2, 0, 2, 4,\ldots$$$ coincideixen i són iguals a $$0$$.
De fet podem observar que la imatge de qualsevol nombre real $$x$$ que considerem coincideix amb les imatges de $$$x + 2, x + 4,\ldots$$$ Direm que la funció és periòdica.
Una funció $$f$$ és periòdica de període $$T$$ si existeix un nombre real positiu $$T$$ tal que per a qualsevol $$x$$ del domini de la funció es té $$$f (x + T) = f (x)$$$
Si $$T$$ és un període de la funció, lògicament també ho serà un múltiple qualsevol de $$T$$. El mínim valor de $$T$$ que compleix la definició anterior es coneix com a període fonamental.
Troba el període fonamental de la funció següent:
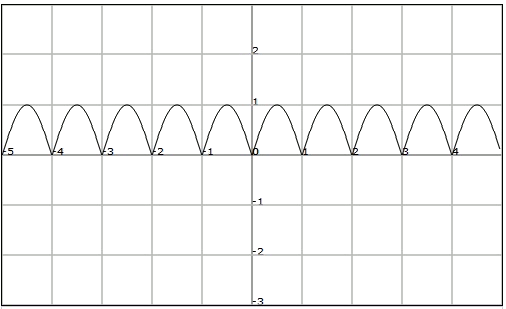
Observem que la funció val $$0$$ per a cada nombre natural, i repeteix el seu comportament entre $$n$$ i $$n + 1$$.
Per tant, en no haver-hi una periodicitat de període menor, tindrem que el període fonamental de $$f$$ és $$T = 1$$.