Funcions parells i senars

Considerem la gràfica de la següent funció f(x)=x2:

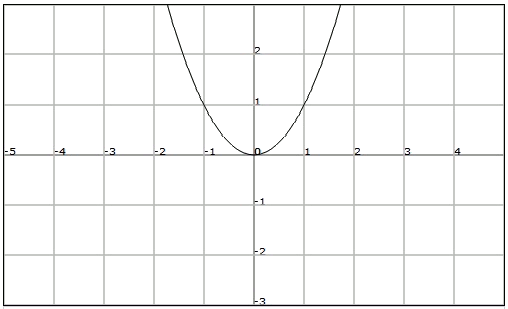
imagen

Observem que qualsevol nombre x i seu oposat −x tenen la mateixa imatge. En aquest cas diem que la funció és parell.

Una funció f és parell si per qualsevol x del domini es verifica: f(x)=f(−x)

Observem que les funcions parells són simètriques respecte de l'eix vertical.

Considerem ara la funció f(x)=x3:

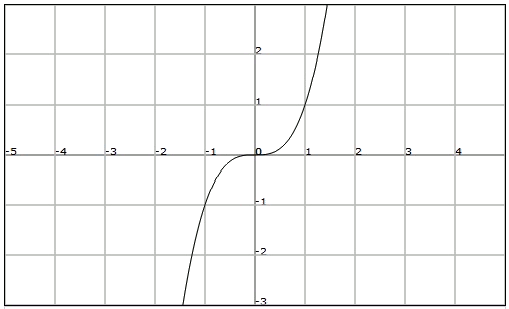
imagen

Observem que qualsevol nombre x i el seu oposat −x tenen imatges oposades. En aquest cas diem que la funció f és senar.

Una funció f és senar si per qualsevol x del domini es verifica: f(x)=−f(−x)

Exemple

Donades les següents funcions, decidiu quines d'elles són parells o senars: f(x)=1x i g(x)=x2−2

Comprovem si les funcions són parells: f(x)=f(−1)⟺1x=1−x⟺1=−1!!g(x)=g(−x)⟺x2−2=(−x)2−2=x2−2 OK 

Comprovem si la funció f és senar (g no ho serà ja que és parell): f(x)=−f(−x)⟺1x=−1−x=1x OK 

Per tant la funció f és senar, i la funció g és parell.