Estudio de la elipse

Una elipse se define como el lugar geométrico de los puntos del plano cuya suma de distancias a dos puntos fijos llamados focos es constante. Su representación gráfica es:

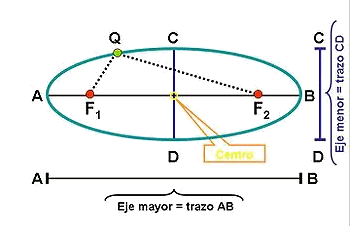
Ahora vamos a definir los elementos que la caracterizan.

• Focos: son los puntos fijos $$F_1$$ y $$F_2$$.
• Eje focal: es la recta que pasa por los dos focos.
• Eje secundario: es la mediatriz del segmento formado por los dos focos.
• Centro: es el punto de intersección del eje focal con el eje secundario.
• Distancia focal: es la distancia entre los dos focos. La semidistancia focal es entonces la mitad y por lo tanto la distancia de cualquier foco al centro (se le llama $$c$$).
• Vértices: es el punto de corte de la elipse con los ejes secundario y focal.
• Eje mayor: es el segmento que une el vértice $$A$$ con el vértice $$B$$.
• Eje menor: es el segmento que une el vértice $$C$$ con el vértice $$D$$.
• Ejes de simetría: son las rectas que contienen alguno de los dos ejes siguientes: el mayor o el menor.
• Centro de simetría: coincide con el centro de la elipse y es el punto intersección de todos los ejes de simetría.

La excentricidad de una elipse (se denota con la letra $$e$$) es la razón entre su semidistancia focal y su semieje mayor.

Este valor se encuentra entre cero y uno dado que $$a>c>0$$. Así pues se tiene: $$$\displaystyle e=\frac{c}{a}$$$ donde $$c$$ es la semidistancia focal y $$a$$ es la longitud del semieje mayor.

La excentricidad indica la forma de una elipse, por eso una elipse será más redondeada cuanto más se aproxime su excentricidad al valor cero. Y será más achatada como más cerca esté del valor $$1$$.