Estudi de l'el·lipse

Una el·lipse es defineix com el lloc geomètric dels punts del pla per als quals és constant la suma de les distàncies a dos punts interiors fixos anomenats focus. La seva representació gràfica és:

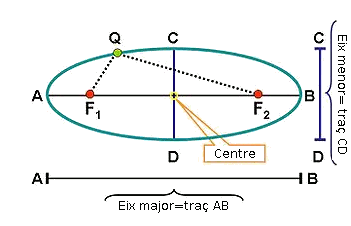
Ara anem a definir els elements que la caracteritzen.

• Focus: són els punts fixos $$F_1$$ i $$F_2$$.
• Eix focal: és la recta que passa pels dos focus.
• Eix secundari: és la mediatriu del segment format pels dos focus.
• Centre: és el punt d'intersecció de l'eix focal amb l'eix secundari.
• Distància focal: és la distància entre els dos focus. La semidistància focal és llavors la meitat i per tant la distància de qualsevol focus al centre (se l'anomena $$c$$).
• Vèrtex: és el punt de tall de l'el·lipse amb els eixos secundari i focal.
• Eix major: és el segment que uneix el vèrtex $$A$$ amb el vèrtex $$B$$.
• Eix menor: és el segment que uneix el vèrtex $$C$$ amb el vèrtex $$D$$.
• Eixos de simetria: són les rectes que contenen algun dels dos eixos següents: el major o el menor.
• Centre de simetria: coincideix amb el centre de l'el·lipse i és el punt intersecció de tots els eixos de simetria.

L'excentricitat d'una el·lipse (es denota amb la lletra $$e$$) és la raó entre la seva semidistància focal i el seu semieix major.

Aquest valor es troba entre zero i 1 donat que $$a>c>0$$. Així doncs es té: $$$\displaystyle e=\frac{c}{a}$$$ on $$c$$ és la semidistància focal i $$a$$ és la longitud del semieix major.

L'excentricitat indica la forma d'una el·lipse, per això una el·lipse serà més arrodonida com més s'aproximi la seva excentricitat al valor zero. I serà més aplanada com més a prop estigui el valor $$1$$.