Una fracción es una cantidad dividida por otra cantidad. Y una unidad fraccionaria es cada una de las partes que se obtienen al dividir una unidad. Pero para ver con claridad estos conceptos vamos a hacer la construcción siguiente:
Tomamos un objeto cualquiera, podría ser un pastel, un lápiz una pizza o incluso una mesa, pero vamos a utilizar un cuadrado azul:
A continuación partiremos este cuadrado en cuatro partes iguales:
Y de estas cuatro partes vamos a colorear una de ellas de rojo:
De esta forma podemos definir la fracción que corresponde a la parte roja, y lo haremos diciendo que el cuadradito rojo es una cuarta parte del cuadrado azul original. Es decir, escribimos la fracción del rectángulo que esta roja como:
$$\dfrac{1}{4}=\dfrac{\mbox{parte del cuadrado que está rojo}}{\mbox{número de partes del cuadrado}}$$
De igual forma podríamos considerar en el cuadrado en seis partes iguales:
Y de estas seis, pintar de rojo cuatro de ellas:
Entonces escribimos la fracción del rectángulo en rojo como: $$\dfrac{4}{6}=\dfrac{\mbox {partes del cuadrado que están en rojo}}{\mbox{número de partes del cuadrado}}$$
Siempre escribiremos las fracciones con esta forma: el número de partes escogidas, sobre una ralla, con el número de partes totales debajo. Y para leerlas, primero decimos el número de arriba y a continuación el de abajo indicándolo con un partido, es decir:
uno partido por dos (una mitad) será: $$\dfrac{1}{2}$$
tres partido por diez: $$\dfrac{3}{10}$$
once partido por seis: $$\dfrac{11}{6}$$
También, si la fracción es partida por dos, hablamos de mitades, entre tres hablamos de tercios, y a partir de cuarto hablamos de cuartos, quintos, etc.:
tres medios: $$\dfrac{3}{2}$$
cinco onceavos: $$\dfrac{5}{11}$$
siete onceavos: $$\dfrac{7}{11}$$
Observemos que el segundo número es el que da nombre a la fracción indocándonos si son medios, tercios u octavos, por este motivo lo llamamos denominador, porque nos da nombre a la fracción: la denomina.
Por otra parte, el primer número nos cuenta en número de partes escogidas (pintadas de rojo) que tenemos, es decir nos numera las distintas fracciones con igual denominador, por esto lo llamamos numerador.
$$$\displaystyle \begin{array}{rcl} \underline{2} & \leftarrow & numerador \\ 3 &\leftarrow & denominador\end{array}$$$
Consideremos ahora la fracción representada por el dibujo siguiente:
Las partes en gris se pueden expresar como $$\dfrac{3}{5}$$ es decir, tres quintos. Este tipo de expresión es equivalente a la división:
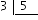
Para verlo más claro empezamos por la fracción un quinto: $$\dfrac{1}{5}$$.
Como ya hemos visto gráficamente, esta fracción equivale a cortar un rectángulo en cinco partes iguales, y de estas tomar solamente una.
Es decir, dividir $$1$$ cuadrado entre $$5$$, $$\dfrac{1}{5}$$, equivale a hacer la división
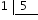
En el caso de tener tres quintos: $$\dfrac{3}{5}$$, ya hemos divido el rectángulo en cinco partes pero hemos tomado tres, por eso, hacemos la división
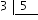
Toda división puede escribirse como una fracción, así como cualquier fracción puede escribirse como división, pero es importante que al escribir las fracciones, los numeradores y los denominadores no pueden ser números decimales ni raíces. Es decir, numerador y denominador deben ser siempre número enteros.
$$\dfrac{9.5}{3}, \dfrac{\sqrt{3}}{4}, \dfrac{2}{1.9}, \dfrac{6}{\sqrt{33}}$$ no serán fracciones. En cambio:
$$\dfrac{-7}{2},\dfrac{8}{5}, \dfrac{-1}{-2}$$ sí serán fracciones.
Según esto se podría pensar que el número 5 no debería ser una fracción, pero lo cierto es que lo es. Esto es debido a que la fracción 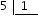$$\dfrac{5}{1}$$ equivale a la división 
, que si la resolvemos nos da:
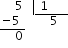
Por lo tanto: $$$\dfrac{5}{1}=5$$$
De igual forma, a cualquier número entero se le puede asignar una fracción cuyo denominador es $$1$$.
Ahora estamos preparados para dar una definición formal de fracción.
Definición: Si $$a$$ y $$b$$ son dos números enteros tales que $$b\neq0$$, llamamos fracción a la expresión $$\frac{a}{b}$$ en la cual $$a$$ es el numerador y $$b$$ el denominador y que equivale al cociente de la división de $$a$$ entre $$b$$.
La principal utilidad de las fracciones es expresar partes de un total. Veamos un ejemplo para empezar:
Para expresar cada uno de los tiempos de un partido de fútbol decimos que es de tres cuartos de hora y escribimos $$\dfrac{3}{4}$$h.
Para saber qué significa tener $$\dfrac{3}{4}$$h debemos dividir la hora en cuatro partes de ellas y tomar tres. Como sabemos que una hora son $$60$$ minutos, partimos $$60$$ entre $$4$$, obtenemos $$15$$, es decir, una cuarta parte de $$60$$ es $$15$$: un cuarto de hora son $$15$$ minutos.
Para obtener lo que valen tres cuartos de hora, debemos multiplicar un cuarto por tres. De esta forma, $$\dfrac{3}{4}$$h son $$15\cdot3=45$$ minutos.
En general, si queremos calcular $$\dfrac{n}{m}$$ de una cantidad $$x$$ (con $$m\neq0$$ necesariamente) tenemos que hacer la cadena de operaciones: $$(x:m)\cdot n$$
Como ya hemos visto en el ejemplo de las horas, $$\dfrac{3}{4}$$ de hora son $$45$$ minutos, ya que, al ser $$1$$h$$=60$$min, hacemos: $$(60:4)\cdot3=(15)\cdot3=15\cdot3=45 \text{ minutos. }$$
Queremos hacer un pozo con una profundidad de $$30$$m por debajo del nivel de tierra, es decir a una altura de $$-30$$m. Cuando hemos perforado exactamente $$\dfrac{2}{3}$$ del pozo nos encontramos una piedra que nos impide continuar la perforación. Queremos saber a cuantos metros de profundidad la hemos encontrado.
Para calcularlo dividimos los $$-30$$m entre $$3$$ y multiplicamos el resultado por $$2$$: $$$(-30:3)\cdot2=-10\cdot2=-20 \text{ m. }$$$
Es decir, hemos encontrado la roca a $$20$$ metros de profundidad.