La variable aleatoria continua $$X$$ sigue una distribución normal $$N(\mu, \sigma)$$, es decir de media $$\mu$$ y desviación típica $$\sigma$$, si cumple que:
- Puede tomar cualquier valor real: $$(-\infty, +\infty)$$
- La función densidad de probabilidad (fpd o pdf del inglés) sigue una curva gaussiana: $$$\displaystyle f(x)=\frac{1}{\sigma \sqrt{2\pi}}\cdot e^{-\frac{1}{2} \Big(\frac{x-\mu}{\sigma}\Big)^2}$$$
Encontrar la función densidad de probabilidad de una variable continua de media $$1,75$$ y desviación típica $$0,2$$ y representarla.
¿De qué podría ser una buena representación esta normal?
$$$\displaystyle f(x)=\frac{1}{0,2 \sqrt{2\pi}}\cdot e^{-\frac{1}{2} \Big(\frac{x-1,75}{0,2}\Big)^2}$$$
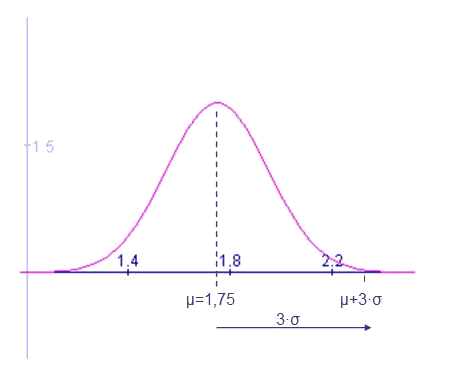
La media y desviación típica proporcionadas hacen que esta variable sea un posible modelo de la altura de los hombres en Barcelona.
Para interpretar la gráfica hay que entender que la probabilidad de que la variable tome un determinado rango de valores es el área por debajo de la curva de la fdp en dicho rango.
- El área total de la fdp es $$1$$:$$$\displaystyle \int_{-\infty}^{+\infty} f(x) \ dx=1$$$
- La fdp es simétrica respecto a $$\mu$$, es decir el área a la derecha de $$\mu$$ es $$0,5$$, y a la izquierda de $$\mu$$ también. O, en el ejemplo anterior, el número de personas por encima de $$1,75$$m es el mismo que el número de gente por debajo de la media.$$$\displaystyle \int_{-\infty}^{\mu} f(x) \ dx=\int_{\mu}^{\infty} f(x) \ dx=\frac{1}{2}$$$
- Además el número de gente más alta que $$1,75 +a$$ es el mismo que el de gente más baja de $$1,75-a$$
$$$\displaystyle \int _{-\infty}^{\mu-a} f(x) \ dx=\int_{\mu+a}^{\infty} f(x) \ dx$$$
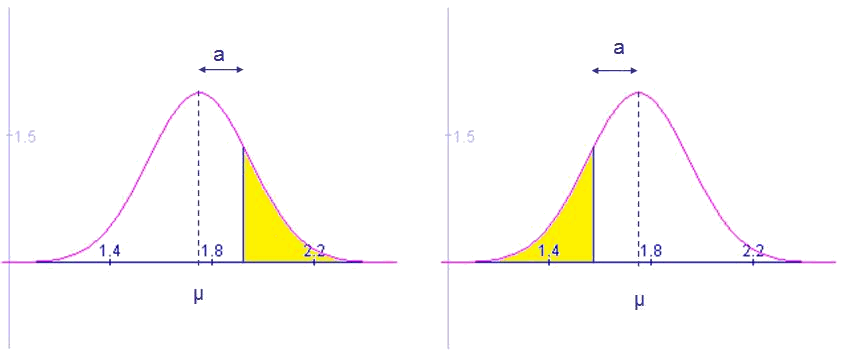
La distribución normal estándar
La distribución normal estándar es la que tiene media $$\mu=0$$ y desviación típica $$\sigma=1$$:
$$$N(0,1)$$$
Su función densidad es:
$$$\displaystyle f(x)=\frac{1}{\sqrt{2\pi}}\cdot e^{-\frac{x^2}{2}}$$$
En la siguiente gráfica vemos su representación:
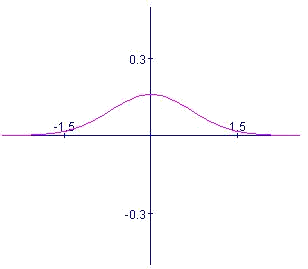
Sobre la distribución normal estándar se puede afirmar:
$$$\displaystyle \int_{-\infty}^{0} f(x) \ dx= \int_{0}^{+\infty} f(x) \ dx = \frac{1}{2} \\ \int_{-\infty}^{-a} f(x) \ dx = \int_{a}^{+\infty} f(x) \ dx $$$
Y, además, cumple todas las propiedades de una función par $$f(-x)=f(x)$$. Dado que la integral mostrada anteriormente no tiene solución analítica se utilizan tablas para calcularla.
A continuación, se puede ver la tabla correspondiente a los valores de la función distribución de probabilidad, es decir:
$$$p(Z \leq z)$$$
La primera posición de la tabla indica la probabilidad de que el resultado del experimento de un valor inferior a cero (la media), y se puede observar que dicha probabilidad es $$0,5$$. La tabla muestra que la probabilidad de un resultado menor que un determinado valor $$z$$ crece a medida que crece $$z$$.
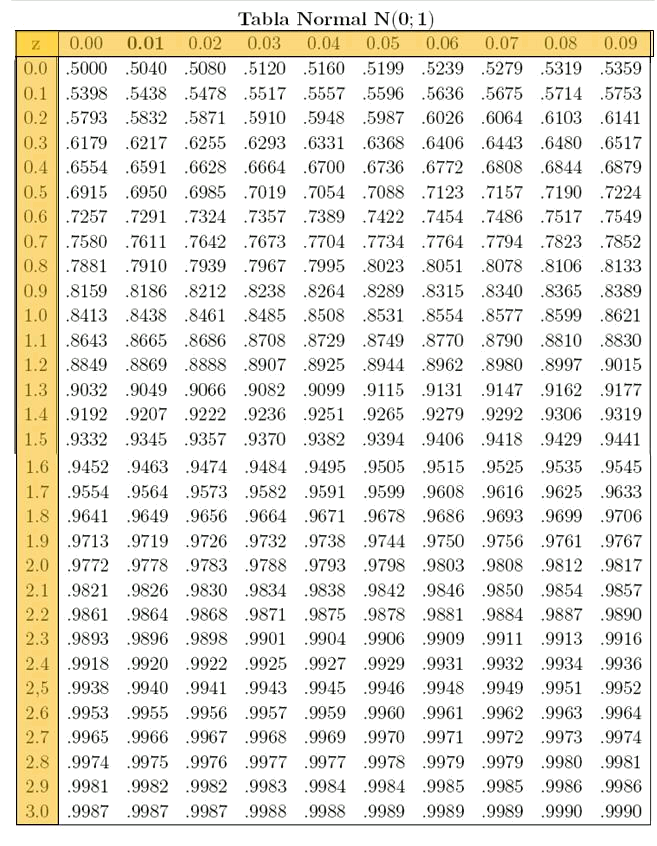
Para interpretar la tabla hay que ver que la columna indica la unidad y la décima de $$z$$, mientras que la fila indica el segundo decimal (la centésima). Es decir, en la primera casilla de la primera fila se ve la probabilidad.
$$$p(Z \leq 0,00)=0,5000$$$
mientras que en la última casilla de la primera fila se ve:
$$$p(Z\leq 0,09)=0,5359$$$
Se puede observar que la tabla sólo da las probabilidades para valores positivos de $$Z$$. Para los valores de $$Z<0$$ se utilizará la geometría, como se podrá ver en los ejemplos que siguen.
Cabe decir que a partir de $$3$$ ($$3$$ veces la desviación típica) la probabilidad es muy cercana a uno $$(0,9987)$$. Por simetría para valores menores a $$-3$$, la probabilidad será prácticamente nula.
Encontrar la probabilidad de que una variable aleatoria $$Z$$ que se modela como $$N(0,1)$$ tenga un valor menor que $$0,94$$.
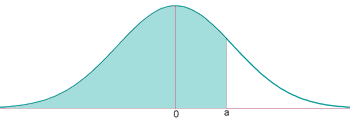
Se mira la fila de $$0,9$$ y la columna de $$0,04$$:
$$$p(Z \leq 0,94)=0,8264$$$
Encontrar la probabilidad de que una variable aleatoria $$Z$$ que se modela como $$N(0,1)$$ tenga un valor mayor que $$0,94$$.
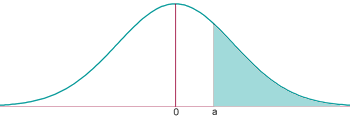
$$$P(Z \geq 0,94)= \mbox{Area}_{\mbox{total}}-P(Z \leq 0,94)\\ P(Z\geq 0,94)=1.0,8264=0,1736$$$
Encontrar la probabilidad de que $$Z$$ esté entre $$0,94$$ y $$1,14$$
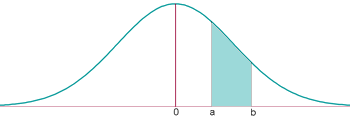
$$$p(0,94 \leq Z \leq 1,14)=p(Z \leq 1,14)-p(Z \leq 0,94) \\ p(0,94 \leq Z \leq 1,14)=0,8728-0,8264=0,0465$$$
Transformación de la normal estándar a cualquier otra normal
¿Qué hay que hacer si se quiere trabajar con una normal distinta a la $$N(0,1)$$?
Si $$Z$$ es una variable aleatoria $$N (0,1)$$ y $$X$$ es $$N (\mu,\sigma)$$ se relacionan por la siguiente expresión:
$$$\displaystyle Z=\frac{X-\mu}{\sigma} \\ X=\sigma\cdot Z + \mu$$$
Se tiene una variable aleatoria de media $$4$$ y desviación estándar $$2$$.
¿Cuál es la probabilidad de que sea mayor que $$6,21$$?
$$$p(X\geq 6,21)=p(\sigma \cdot Z+\mu \geq 6,21)\\ p(X\geq 6,21)= p(Z\geq \frac{6,21-4}{2})=p(Z\geq 1,105) \\ p(Z\geq 1,105) = 1- p(Z\leq 1,105)=1-0,8531=0,1469$$$
De esta forma, sólo serán necesarias las tablas para la normal $$N(0,1)$$
Aproximación de la distribución binomial a partir de una normal
Para $$n$$ suficientemente grande, el cálculo de una binomial $$B(n,p)$$ puede resultar complicado.
Por ello se utiliza una normal:
$$$N(\mu=np, \sigma =\sqrt{npq}) \approx B(n,p)$$$
Así pues, para tratar la binomial que modela los $$100$$ lanzamientos de una moneda se puede utilizar:
$$$N(100 \cdot 0,5 , \sqrt{100\cdot 0,5 \cdot 0,5})=N(50, 5)$$$
De esta forma se podrá evitar el cálculo con exponentes elevados que supone el uso de una binomial, y se podrán utilizar las tablas de la normal $$N(0,1)$$.
