La distribució normal o Gaussiana

La variable aleatòria contínua $X$ segueix una distribució normal $N (μ, σ)$ , és a dir de mitjana $μ$ i desviació típica $σ$ , si compleix que:

Pot prendre qualsevol valor real: $(- \infty, + \infty)$
La funció densitat de probabilitat (fpd o pdf de l'anglès)segueix una corba gaussiana:

$f (x) = \frac{1}{σ \sqrt{2 π}} \cdot e^{- \frac{1}{2} (\frac{x - μ}{σ})^{2}}$

Exemple

Trobar la funció densitat de probabilitat d'una variable contínua de mitjana $1, 75$ i desviació típica $0, 2$ i representar-la.

De què podria ser una bona representació aquesta normal?

$f (x) = \frac{1}{0, 2 \sqrt{2 π}} \cdot e^{- \frac{1}{2} (\frac{x - 1, 75}{0, 2})^{2}}$

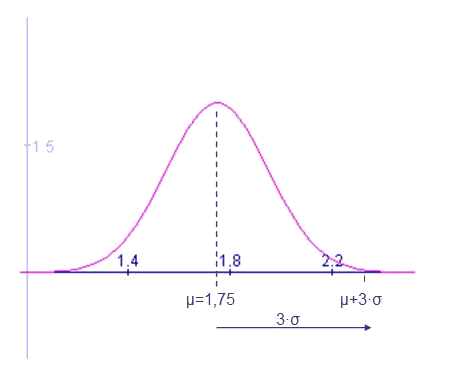
imagen

La mitjana i desviació típica proporcionades fan que aquesta variable sigui un possible model de l'alçada dels homes a Barcelona.

Per interpretar la gràfica s'ha d'entendre que la probabilitat que la variable prengui un determinat rang de valors és l'àrea per sota de la corba de la funció de probabilitat en aquest rang.

L'àrea total de la funció de probabilitat és $1$ : $\int_{- \infty}^{+ \infty} f (x) d x = 1$
La funció de probabilitat és simètrica respecte a $μ$ , és a dir l'àrea a la dreta de $μ$ és $0, 5$ , i a l'esquerra de $μ$ també. O, en l'exemple anterior, el nombre de persones per sobre de $1, 75$ m és el mateix que el nombre de gent per sota de la mitjana. $\int_{- \infty}^{μ} f (x) d x = \int_{μ}^{\infty} f (x) d x = \frac{1}{2}$
A més el nombre de gent més alta que $1, 75 + a$ és el mateix que el de gent més baixa de $1, 75 - a$

$\int_{- \infty}^{μ - a} f (x) d x = \int_{μ + a}^{\infty} f (x) d x$

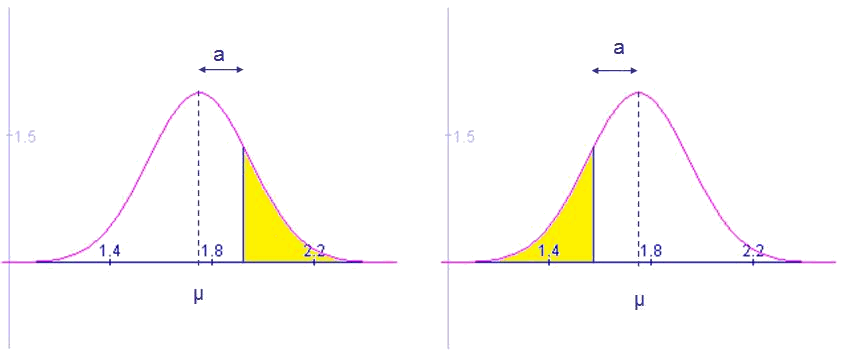
imagen

La distribució normal estàndard

La distribució normal estàndard és la que té mitjana $μ = 0$ i desviació típica $σ = 1$ :

$N (0, 1)$

La seva funció densitat és:

$f (x) = \frac{1}{\sqrt{2 π}} \cdot e^{- \frac{x^{2}}{2}}$

En la següent gràfica veiem la seva representació:

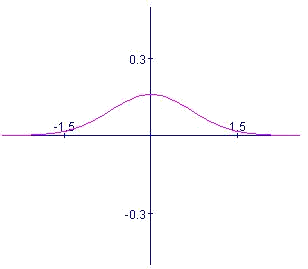
imagen

Sobre la distribució normal estàndard es pot afirmar:

$\int_{- \infty}^{0} f (x) d x = \int_{0}^{+ \infty} f (x) d x = \frac{1}{2} \int_{- \infty}^{- a} f (x) d x = \int_{a}^{+ \infty} f (x) d x$

I, a més, compleix totes les propietats d'una funció parell $f (- x) = f (x)$ . Atès que la integral mostrada anteriorment no té solució analítica s'utilitzen taules per calcular-la.

A continuació, es pot veure la taula corresponent als valors de la funció distribució de probabilitat, és a dir:

$p (Z \leq z)$

La primera posició de la taula indica la probabilitat que el resultat de l'experiment d'un valor inferior a zero (la mitjana), i es pot observar que aquesta probabilitat és $0, 5$ . La taula mostra que la probabilitat d'un resultat menor que un determinat valor $z$ creix a mesura que creix $z$ .

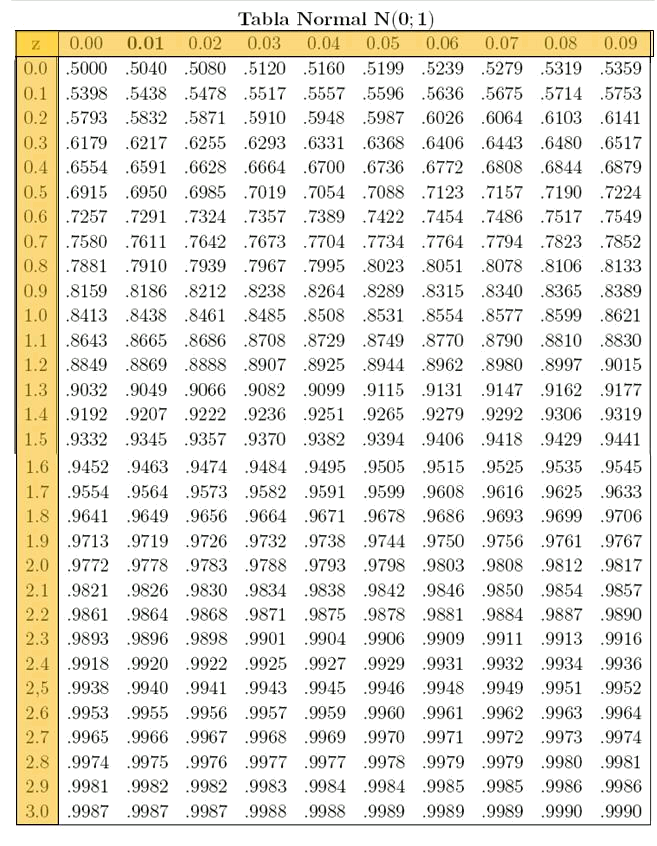
imagen

Per interpretar la taula s'ha de veure que la columna indica la unitat i la desena de $z$ , mentre que la columna indica el segon decimal (la centèsima). És a dir, a la primera casella de la primera fila es veu la probabilitat

$p (Z \leq 0, 00) = 0, 5000$

mentre que en la darrera casella de la primera fila es veu:

$p (Z \leq 0, 09) = 0, 5359$

Es pot observar que la taula només dóna les probabilitats per a valors positius de $Z$ . Per als valors de $Z < 0$ s'utilitzarà la geometria, com es podrà veure en els exemples que segueixen.

Val a dir que a partir de $3$ ( $3$ vegades la desviació típica) la probabilitat és molt propera a un $(0, 9987)$ . Per simetria per a valors menors a $- 3$ , la probabilitat serà pràcticament nul·la.

Exemple

Trobar la probabilitat que una variable aleatòria $Z$ que es modela com $N (0, 1)$ tingui un valor menor que $0, 94$ .

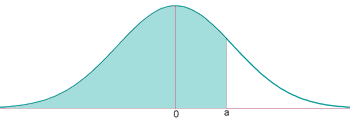
imagen

Es mira la fila de $0, 9$ i la columna de $0, 04$ :

$p (Z \leq 0, 94) = 0, 8264$

Exemple

Trobar la probabilitat que una variable aleatòria $Z$ que es modela com $N (0, 1)$ tingui un valor més gran que $0, 94$ .

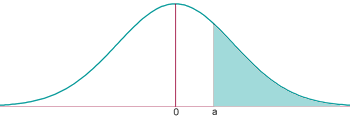
imagen

$P (Z \geq 0, 94) = {Area}_{total} - P (Z \leq 0, 94) P (Z \geq 0, 94) = 1.0, 8264 = 0, 1736$

Exemple

Trobar la probabilitat que $Z$ estigui entre $0, 94$ i $1, 14$

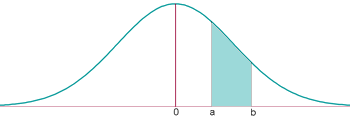
imagen

$p (0, 94 \leq Z \leq 1, 14) = p (Z \leq 1, 14) - p (Z \leq 0, 94) p (0, 94 \leq Z \leq 1, 14) = 0, 8728 - 0, 8264 = 0, 0465$

Transformació de la normal estàndard a qualsevol altra normal

Què cal fer si es vol treballar amb una normal diferent de la $N (0, 1)$ ?

Si $Z$ és una variable aleatòria $N (0, 1)$ i $X$ és $N (μ, σ)$ es relacionen per la següent expressió:

$Z = \frac{X - μ}{σ} X = σ \cdot Z + μ$

Exemple

Tenim una variable aleatòria de mitjana $4$ i desviació estàndard $2$ .

Quina és la probabilitat que sigui més gran que $6, 21$ ?

$p (X \geq 6, 21) = p (σ \cdot Z + μ \geq 6, 21) p (X \geq 6, 21) = p (Z \geq \frac{6, 21 - 4}{2}) = p (Z \geq 1, 105) p (Z \geq 1, 105) = 1 - p (Z \leq 1, 105) = 1 - 0, 8531 = 0, 1469$

D'aquesta manera, només seran necessàries les taules per a la normal $N (0, 1)$ .

Aproximació de la distribució binomial a partir d'una normal

Per $n$ prou gran, el càlcul d'una binomial $B (n, p)$ pot resultar complicat.

Per això s'utilitza una normal:

$N (μ = n p, σ = \sqrt{n p q}) \approx B (n, p)$

Així doncs, per tractar la binomial que modela els $100$ llançaments d'una moneda es pot utilitzar:

$N (100 \cdot 0, 5, \sqrt{100 \cdot 0, 5 \cdot 0, 5}) = N (50, 5)$

D'aquesta manera es podrà evitar el càlcul amb exponents elevats que suposa l'ús d'una binomial, i es podran utilitzar les taules de la normal $N (0, 1)$ .