Empecemos considerando el siguiente ejemplo:
Una fábrica de tornillos tiene dos máquinas, la $$M1$$, que es más antigua, y hace el $$75\%$$ de todos los tornillos, y la $$M2$$, más nueva pero pequeña, que hace el $$25\%$$ de los tornillos. La $$M1$$ hace un $$4\%$$ de tornillos defectuosos, mientras que la $$M2$$ tan sólo hace un $$2\%$$ de tornillos defectuosos. Si escogemos un tornillo al azar, ¿qué probabilidad hay de que salga defectuoso?
Podemos resolver el problema utilizando el teorema de la probabilidad total, que no es otra cosa que utilizar un diagrama en árbol para resolverlo.
Miremos ahora el problema desde otro punto de vista. Si sabemos que un tornillo es defectuoso, ¿qué probabilidad hay de que haya sido fabricado por la máquina $$M1$$?
Es decir, nos estamos preguntando por la probabilidad condicionada $$P(M1/D)$$. Por un lado, por la definición de probabilidad condicionada, tenemos que:
$$$P(M1/D)=\dfrac{P(M1\cap D)}{P(D)}$$$
Por otro lado, si representamos nuestro problema en un diagrama en árbol, vemos que podemos calcular $$P(M1\cap D)$$, ya que es la probabilidad de la rama marcada: ser fabricado por $$M1$$ y también ser defectuoso.
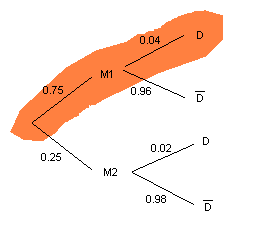
Si tenemos en cuenta, además, el teorema de la probabilidad total: $$$P(D) = P(M1)\cdot P(D/M1) + P(M2)\cdot P(D/M2)$$$ llegamos finalmente a que: $$$P(M1/D)=\dfrac{P(M1)\cdot P(D/M1)}{P(M1)\cdot P(D/M1) + P(M2)\cdot P(D/M2)}$$$
En nuestro ejemplo, $$$P(M1/D)=\dfrac{0,75\cdot 0,04}{0,75\cdot 0,04 + 0,25\cdot 0,02}=0,857$$$
Lo que hemos hecho para resolver este problema, lo podemos enunciar de forma general como el teorema de Bayes.
-
Teorema de Bayes:
Sea $$A_1,A_2,\ldots, A_n$$ un sistema completo de sucesos i $$B$$ un suceso cualquiera asociado al mismo experimento. Entonces, se cumple que: $$$ P(A_i/B)=\dfrac{P(A_i)\cdot P(B/A_i)}{P(A_1)\cdot P(B/A_1)+\ldots+P(A_n)\cdot P(B/A_n)}$$$
Veamos cómo aplicarlo.
Tenemos tres cajas con bombillas. La primera contiene $$10$$ bombillas, de las cuales hay cuatro fundidas; en la segunda hay seis bombillas, y tan sólo una fundida, y en la tercera hay tres bombillas fundidas de un total de ocho. Si cogemos una bombilla fundida, ¿cuál es la probabilidad de que sea de la caja $$1$$?
Recordemos que $$C1$$, $$C2$$, $$C3$$ representan las cajas $$1$$, $$2$$ y $$3$$. También $$F = $$ "bombilla fundida", por lo que $$\overline{F}=$$ "bombilla no fundida".
Ahora sólo nos interesa la rama superior de nuestro diagrama en árbol.
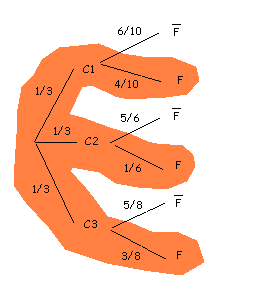
Nos interesa $$P(C1/F)$$. Por el teorema de Bayes, $$$ P(C1/F)=\dfrac{P(C1)\cdot P(F/C1)}{P(C1)\cdot P(F/C1)+P(C2)\cdot P(F/C2)+P(C3)\cdot P(F/C3)}$$$
En nuestro caso, $$$P(C1/F)=\dfrac{\dfrac{1}{3}\cdot \dfrac{4}{10}}{\dfrac{1}{3}\cdot \dfrac{4}{10} + \dfrac{1}{3}\cdot \dfrac{1}{6}+\dfrac{1}{3}\cdot \dfrac{3}{8}}=\dfrac{\dfrac{4}{30}}{\dfrac{113}{360}}=\dfrac{48}{113}=0,425$$$
es decir, un $$42,5\%$$.
En un congreso se reúnen $$250$$ médicos de Europa, de los cuales $$115$$ son alemanes; $$65$$, franceses, y $$70$$ ingleses. De estos médicos, el $$75\%$$ de los alemanes, el $$60\%$$ de los franceses y el $$65\%$$ de los ingleses están a favor de utilizar una nueva vacuna para la gripe. Si escogemos un médico al azar, y está a favor de aplicar la vacuna, ¿cuál es la probabilidad de que sea francés?
Consideremos los siguientes sucesos: $$A =$$ "médico alemán", $$F =$$ "médico francés", $$I =$$ "médico inglés", así como $$V =$$ "estar a favor de la vacuna" (y por lo tanto, $$ \overline{V}=$$ "estar en contra de la vacuna").
Representamos nuestro problema en un diagrama en árbol.
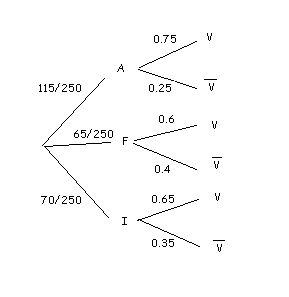
Nos estamos preguntando por $$P(F/V)$$. Por el teorema de Bayes, $$$ P(F/V)=\dfrac{P(F)\cdot P(V/F)}{P(A)\cdot P(V/A)+P(F)\cdot P(V/F)+P(I)\cdot P(V/I)}$$$
En nuestro caso, $$$P(F/V)=\dfrac{\dfrac{65}{250}\cdot 0,6}{\dfrac{115}{250}\cdot 0,75 + \dfrac{65}{250}\cdot 0,6+\dfrac{70}{250}\cdot 0,65} =0,228$$$
