Comencem considerant el següent exemple:
Una fàbrica de cargols té dues màquines, la $$M1$$, que és més antiga, i fa el $$75\%$$ de tots els cargols, i la $$M2$$, més nova però petita, que fa el $$25\%$$ dels cargols. La $$M1$$ fa un $$4\%$$ de cargols defectuosos, mentre que la $$M2$$ tan sols fa un $$2\%$$ de cargols defectuosos. Si escollim un cargol a l'atzar, quina probabilitat hi ha de que surti defectuós?
Podríem resoldre el problema utilitzant el teorema de la probabilitat total, que no era res més que utilitzar un diagrama en arbre per a resoldre'l.
Mirem ara el problema des d'un altre punt de vista. Si sabem que un cargol és defectuós, quina probabilitat hi ha que hagi estat fabricat per la màquina M1?
És a dir, ens estem preguntant per la probabilitat condicionada $$P(M1/D)$$. D'una banda, per la definició de probabilitat condicionada, tenim que:
$$$P(M1/D)=\dfrac{P(M1\cap D)}{P(D)}$$$
D'altra banda, si representem el nostre problema en un diagrama en arbre, veiem que podem calcular $$P(M1\cap D)$$, ja que és la probabilitat de la branca marcada: ser fabricat per $$M1$$ i també ser defectuós.
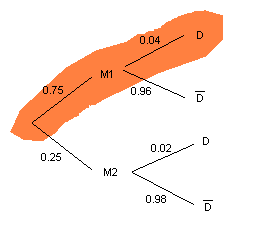
Si tenim en compte, a més, el teorema de la probabilitat total: $$$P(D) = P(M1)\cdot P(D/M1) + P(M2)\cdot P(D/M2)$$$ arribem finalment a que: $$$P(M1/D)=\dfrac{P(M1)\cdot P(D/M1)}{P(M1)\cdot P(D/M1) + P(M2)\cdot P(D/M2)}$$$
En el nostre exemple, $$$P(M1/D)=\dfrac{0,75\cdot 0,04}{0,75\cdot 0,04 + 0,25\cdot 0,02}=0,857$$$
El que hem fet per a resoldre aquest problema, ho podem enunciar de forma general com el teorema de Bayes.
-
Teorema de Bayes:
Sigui $$A_1,A_2,\ldots, A_n$$ un sistema complet de successos i $$B$$ un succés qualsevol associat al mateix experiment. Llavors, es compleix que: $$$ P(A_i/B)=\dfrac{P(A_i)\cdot P(B/A_i)}{P(A_1)\cdot P(B/A_1)+\ldots+P(A_n)\cdot P(B/A_n)}$$$
Vegem com aplicar-lo.
Tenim tres caixes amb bombetes. La primera conté $$10$$ bombetes, de les quals hi ha quatre foses, en la segona hi ha sis bombetes, i tan sols una fosa, i en la tercera hi ha tres bombetes foses d'un total de vuit. Si agafem una bombeta fosa, quina és la probabilitat que sigui de la caixa $$1$$?
Recordem que $$C1$$, $$C2$$, $$C3$$ representen les caixes $$1$$, $$2$$ i $$3$$. També $$F = $$ "bombeta fosa", de manera que $$\overline{F}=$$ "bombeta no fosa".
Ara només ens interessa la branca superior del nostre diagrama en arbre.
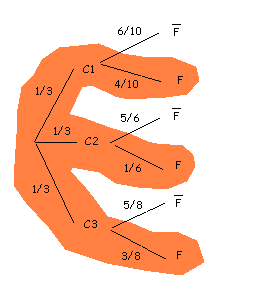
Ens interessa $$P(C1/F)$$. Pel teorema de Bayes, $$$ P(C1/F)=\dfrac{P(C1)\cdot P(F/C1)}{P(C1)\cdot P(F/C1)+P(C2)\cdot P(F/C2)+P(C3)\cdot P(F/C3)}$$$
En el nostre cas, $$$P(C1/F)=\dfrac{\dfrac{1}{3}\cdot \dfrac{4}{10}}{\dfrac{1}{3}\cdot \dfrac{4}{10} + \dfrac{1}{3}\cdot \dfrac{1}{6}+\dfrac{1}{3}\cdot \dfrac{3}{8}}=\dfrac{\dfrac{4}{30}}{\dfrac{113}{360}}=\dfrac{48}{113}=0,425$$$
és a dir, un $$42,5\%$$.
En un congrés es reuneixen $$250$$ metges d'Europa, dels quals $$115$$ són alemanys, $$65$$, francesos, i $$70$$ anglesos. D'aquests metges, el $$75\%$$ dels alemanys, el $$60\%$$ dels francesos i el $$65\%$$ dels anglesos estan a favor d'utilitzar una nova vacuna per la grip. Si escollim un metge a l'atzar, i està a favor d'aplicar la vacuna, quina és la probabilitat que sigui francès?
Considerem els següents esdeveniments: $$A =$$ "metge alemany", $$F =$$ "metge francès", $$I =$$ "metge anglès", així com $$V =$$ "estar a favor de la vacuna" (i per tant, $$ \overline{V}=$$ "estar en contra de la vacuna").
Representem el nostre problema en un diagrama en arbre.
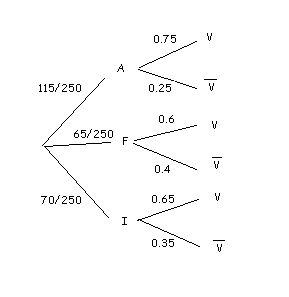
Ens estem preguntant per $$P(F/V)$$. Pel teorema de Bayes, $$$ P(F/V)=\dfrac{P(F)\cdot P(V/F)}{P(A)\cdot P(V/A)+P(F)\cdot P(V/F)+P(I)\cdot P(V/I)}$$$
En el nostre cas, $$$P(F/V)=\dfrac{\dfrac{65}{250}\cdot 0,6}{\dfrac{115}{250}\cdot 0,75 + \dfrac{65}{250}\cdot 0,6+\dfrac{70}{250}\cdot 0,65} =0,228$$$