El tetràedre és una figura formada a partir de $$4$$ triangles equilàters.
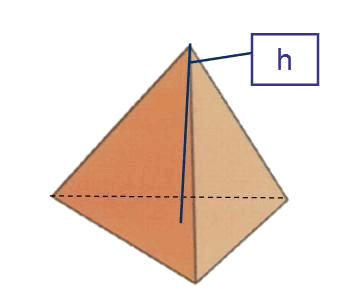
Així doncs, per calcular l'àrea del tetràedre: $$$A_{tetràedre}=4\cdot \dfrac{a\cdot h}{2}=2 \cdot a \cdot h$$$
Atès que els triangles que componen el tetràedre són equilàters, es pot expressar la seva altura $$h$$ en funció de la seva base: $$$a^2=\Big(\dfrac{a}{2}\Big)^2+h^2 \\ h^2=a^2\Big(\dfrac{3}{4}\Big) \\ h= a \cdot \dfrac{\sqrt{3}}{2}$$$
I l'àrea del tetràedre resulta ser: $$$A_{tetràdre}=\dfrac{a \cdot a \cdot \dfrac{\sqrt{3}}{2}}{2}=\dfrac{a^2 \cdot \sqrt{3}}{4}=a^2 \cdot \sqrt{3}$$$
Finalment, l'expressió del volum del tetràedre regular és: $$$V=\dfrac{ \sqrt{2}}{12}\cdot a^3$$$